Câu 1
Cho tứ diện \(ABCD\) có \(AB=6; CD = 8\) và tất cả các cạnh còn lại đều bằng \(\sqrt{74}\). Thể tích khối tứ diện \(ABCD\) bằng
A. 56.
B. 168.
C. \(6.\sqrt{74}\)
D. 112
Lời giải
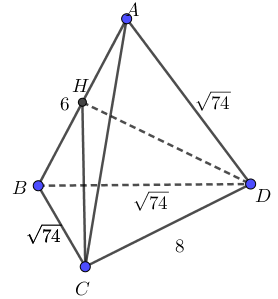
Gọi \(H\) là trung điểm \(AB\). Do \(BC=CA=DB=DA=\sqrt{74}\) nên hai tam giác \(ABC\) và \(ABD\) là cân. do đó ta có \(CH, DH \) cùng vuông góc \(AB\), nói cách khác \(AB\) vuông góc \(HCD\)
Xét chóp \(A.HCD\), ta có đường cao \(AH=\dfrac{6}{2}=3\)
\(HC=HD=\sqrt{AD^2-AH^2}=\sqrt{65}\)
Như vậy, tam giác \(HCD\) có 3 cạnh có độ dài lần lượt là: \(8; \sqrt{65}; \sqrt{65}\) nên áp dụng công thức Hê rông ta có ngay
\(S_{HCD}=28\)
Suy ra: \(V_{A.HCD}=\dfrac{1}{3}.AH.S_{HCD}=28\)
Mặt khác: \(V_{ABCD}=2V_{A.HCD}=2.28=56\)
Vậy, chọn A.
Câu 2
Cho lăng trụ \(ABC.A’B’C’\) có \(ABC\) là tam giác vuông cân tại \(A\), \(AB = a\sqrt 2 \), \(A’\) cách đều \(A, B, C\) và góc giữa hai mặt phẳng \((ABC)\) và \((BCC’B’)\) bằng \(45^0\). Thể tích của khối lăng trụ là
A. \({a^3}\) B. \(2\sqrt 2 {a^3}\) C. \(\sqrt 2 {a^3}\) D. \(\dfrac{{{a^3}}}{3}\)
Lời giải
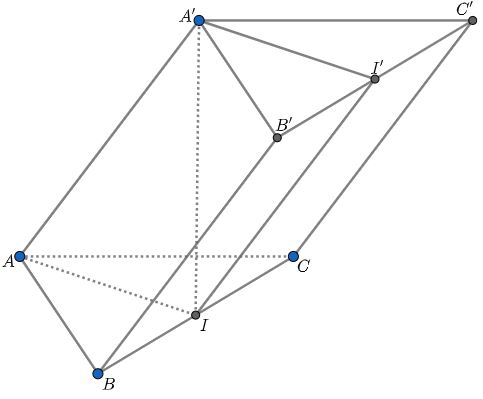
Do \(ABC\) là tam giác vuông tại \(A\) nên tâm đường tròn ngoại tiếp của nó là trung điểm \(I\) của \(BC\). Mặt khác theo giả thiết \(A^\prime A=A^\prime B = A^\prime C\) nên ta có \(IA^\prime\) là trục đường tròn ngoại tiếp tam giác \(ABC\) hay nói cách khác ta có \(A^\prime I\) vuông góc với \((ABC)\) tại \(I\)
Đề bài cho góc giữa \(BCC^\prime B^\prime\) và \(ABC\) là \(45^0\) ta có thể xem như góc giữa \(BCC’B’\) và \(A’B’C’\) là \(45^0\).
Việc xác định góc giữa \(BCC’B’\) và \(A’B’C’\) dễ thấy đó là góc \(II’A’\) với \(I’\) là trung điểm của \(B’C’\) (đây giống như một bản sao của I trên mặt phẳng \(A’B’C’\)
Như vậy \(\widehat{II’A’}=45^0\).
Tam giác \(ABC\) vuông cân tại \(A\) mà \(AB=a\sqrt2\) nên \(BC=2a\).
Do đó \(A’I’=AI=\dfrac{1}{2}BC=a\). Từ đó suy ra \(IA’=a\) (do tam giác \(IA’I’\) vuông tại \(A’\) và \(\widehat{II’A’}=45^0\).
Tới đây ta đã có đường cao, còn diện tích \(ABC\) thì đơn giản rồi, tất nhiên \(S_{ABC}=\dfrac{1}{2}.AB.AC=a^2\)
Vậy: \(V_{ABC.A’B’C’}=a.a^2=a^3\)
Lời bình:
Bài này, độc giả có thể xác định góc giữa \(BCC’B’\) và \(ABC\) bằng cách khác là dựng đường \(I’H\) song song với \(A’I\) tại một điểm \(H\) nằm trên đường thẳng \(AI\). cũng khá vất vả để thấy điều này, từ đó với cách ở trên ta nhận thấy rõ thêm ý nghĩa của 2 mặt đáy lăng trụ là bản sao của nhau



