Đây là đề và đáp số (lời giải gợi ý) thi Học kì I môn Toán lớp 10 trường THPT Hùng Vương TpHCM 2021-2022, mời các bạn xem thử nha
Câu 1. (2đ)
Cho hàm số \(y=x^{2}-6 x+8\) có đồ thị là Parabol (P).
a. Lập bảng biến thiên và vẽ đồ thị (P) của hàm số.
b. Dựa vào đồ thị (P), tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=x^{2}-6x+8\) trên đoạn \([0 ; 4]\).
Câu 2. (1đ)
Giải và biện luận phương trình: \(\left(m^{2}-3 m+2\right) x-m+2=0\)
Câu 3. (1đ)
Định giá trị của tham số \(m\) để phương trình \(m x^{2}+2(m+1) x+m-2=0\) có 2 nghiệm phân biệt \(x_1; x_2\) thỏa mãn: \(\dfrac{1}{x_{1}}+\dfrac{1}{x_{2}}=m+3\)
Câu 4. (1đ)
Giải phương trình: \(\sqrt{x^{2}+5 x+1}=2 x-1\)
Câu 5. (1đ)
Giải hệ phương trình: \(\left\{\begin{array}{l} x+y=2 \\ x^{2}+y^{2}=10 \end{array} \right.\)
Câu 6. (2đ)
Trong mặt phẳng tọa độ \(Oxy\), cho hình bình hành \(ABCD\) với \(A(-2;1)\); \(B(3;-2)\); \(C(0;3)\)
a. Tìm tọa độ đỉnh \(D\) và tọa độ tâm \(I\) của hình bình hành \(ABCD\)
b. Tìm tọa độ trọng tâm của tam giác \(ABC\)
Câu 7. (2đ)
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) với \(A(-4 ;-3) \), \(B(4 ; 0)\), \(C(-1;5)\)
a. Chứng minh rằng tam giác \(ABC\) cân tại \(A\)
b. Tìm tọa độ điểm \(M\) trên trục tung \(Oy\) sao cho tam giác \(MAC\) vuông tại \(M\).
— HẾT —
Gợi ý-lời giải-đáp số
Câu 1.
a. Khá đơn giản, đồ thị như hình vẽ bên
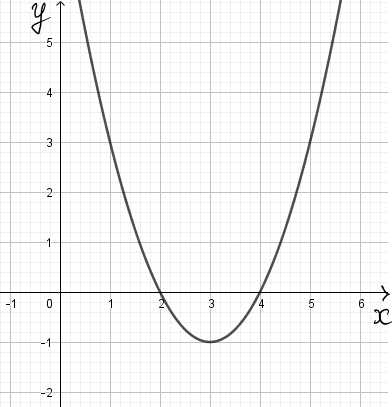
Câu 1. ý b.
Khi \(x=0\) thì \(y=8\) do vậy đồ thị hàm số cắt \(Oy\) tại \((0;8)\).
Từ đồ thị hàm số, trên đoạn [0;4] ta thấy GTLN của hàm số là \(8\) đạt tại \(x=0\) còn giá trị nhỏ nhất của hàm số là \(-1\) đạt tại \(x=3\)
Câu 2.
Phương trình tương đương \(\left(m^{2}-3 m+2\right) x=m-2\)
Đây là phương trình dạng \(ax=b\)
Kết quả ta có: Khi \(m=2\) tập nghiệm phương trình là \(S=R\)
Khi \(m=1\) phương trình vô nghiệm (tập nghiệm là \(S=\emptyset\) )
Khi \(m\neq 1\) và \(m \neq 2\) phương trình có nghiệm duy nhất \(x=\dfrac{1}{m-1}\)
Câu 3.
Đầu tiên là điều kiện để p.tr có 2 nghiệm phân biệt \(x_1; x_2\)
đó là \(m \neq 0\) và \((m+1)^2-m(m-2) >0\) tức là \(m>\dfrac{-1}{4}\) và \(m \neq 0\)
Lúc đó theo định lý Viet ta có:
\(x_1 + x_2 = \dfrac{-2(m+1)}{m}\)
\(x_{1}.x_{2}=\dfrac{m-2}{m}\)
Từ điều kiện đề bài ta có: \(x_1 + x_2 =(m+3).x_{1}x_2\)
Tương đương: \( \dfrac{-2(m+1)}{m} =(m+3). \dfrac{m-2}{m} \)
Giải được \(m=-4\) hoặc \(m=1\). So điều kiện ta chỉ nhận kết quả \(m=1\)
Câu 4.
Dùng công thức \(\sqrt{A}=B\) giải được nghiệm duy nhất \(x=3\)
Câu 5.
Đây là hệ p.tr đối xứng loại (I), chỉ cần đặt \(S=x+y\) và \(P=xy\) đưa về hệ quen thuộc.
Kết quả nghiệm là: \((3;-1)\) và \((-1;3)\)
Câu 6.
a. Dùng \(\overrightarrow{AB}=\overrightarrow{DC}\) giải được kết quả \(D(-5;6)\) ; còn tọa độ \(I\) thì chẳng qua là trung điểm đoạn \(AC\) nên \(I(-1;2)\)
b. Tọa độ trọng tâm \(G\) của tam giác \(ABC\) là: \(G\left(\dfrac{1}{3}; \dfrac{2}{3}\right) \)
Câu 7.
a. Tính độ dài \(AB\) và \(AC\) ta được \(AB=AC=\sqrt{73}\) nên tam giác \(ABC\) cân tại A.
b. \(M\) thuộc \(Oy\) nên \(M(0;y)\), dùng điều kiện \(\overrightarrow{MA}.\overrightarrow{MC}=0\) giải được \(M(0;1-2\sqrt3)\) hoặc \(M(0;1+2\sqrt3)\)




