Web gửi tặng đến các bạn đề thi học kì 2 môn Toán năm học 2020-2021 một số trường, một số đề có kèm đáp án-lời giải chi tiết bên dưới để giúp các bạn chuẩn bị tốt nhất cho các kì thi.
1. Đề Trần Khai Nguyên
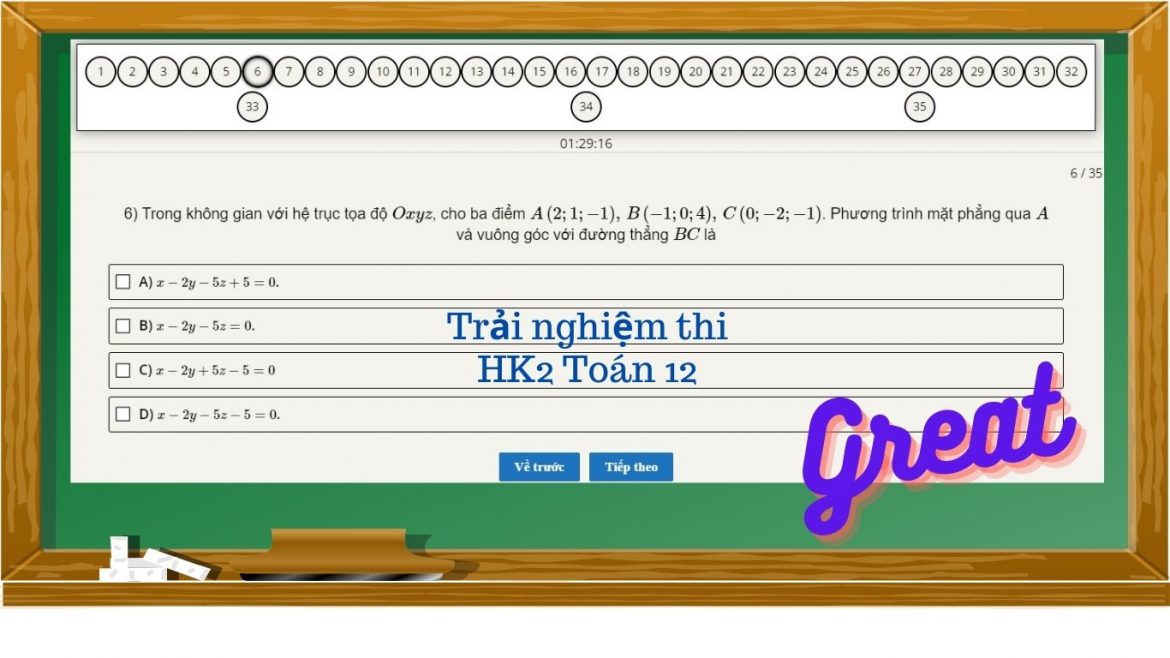
Đề gồm 35 câu trắc nghiệm mời các bạn có thể làm trực tiếp tại đây và nhận kết quả nha
5
2. Đề Trung học Thực hành ĐHSP
Bạn có thể nhấn vào mũi tên bên phải để phóng to và tải tài liệu về hoặc bấm nút tải về bên dưới nhé
Đáp án và giải chi tiết đề này tại đây nha
3. Đề thi HK2 2019 2020 Nguyễn Du, Trần Khai Nguyên, Lê Hồng Phong, Nguyễn Hiền
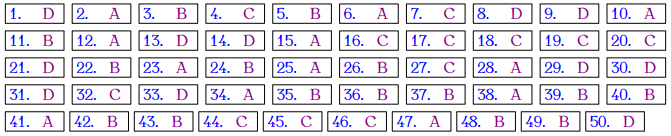
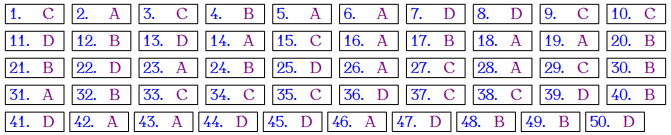
Đáp án các đề này là: