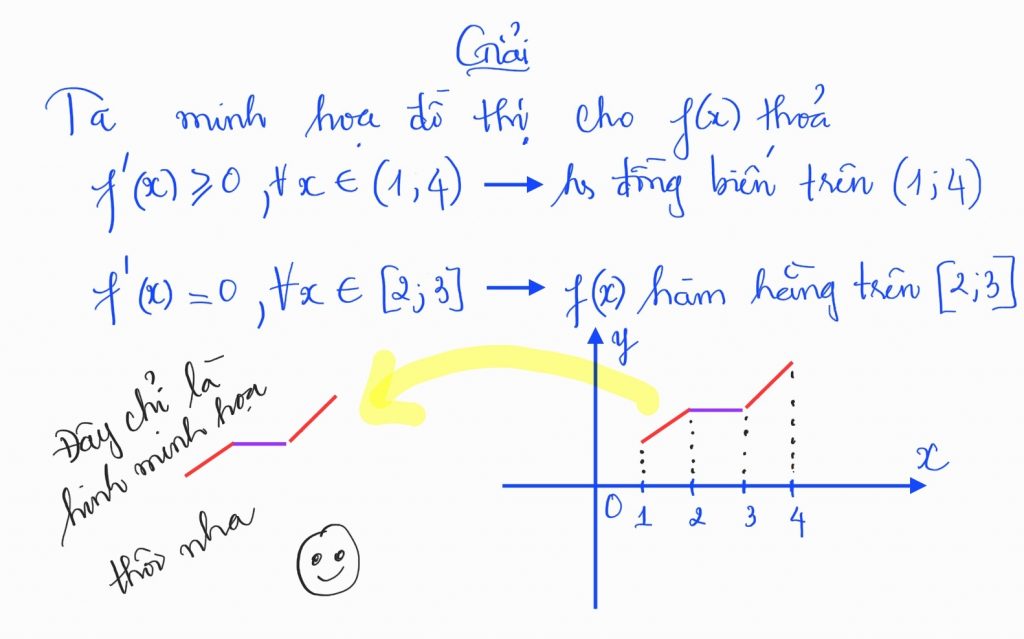
Đây là một câu hỏi đến từ một học sinh chăm chỉ, tác giả đưa lên đây để minh họa một tình huống học sinh thường ít để khi nói về tính đơn điệu của hàm số. Cụ thể, chúng ta đã quen với:
\(f^\prime (x) >0, \forall x \in D \Rightarrow f(x) \) đồng biến trên D
và ngược lại; \(f^\prime (x) <0, \forall x \in D \Rightarrow f(x) \) nghịch biến trên D
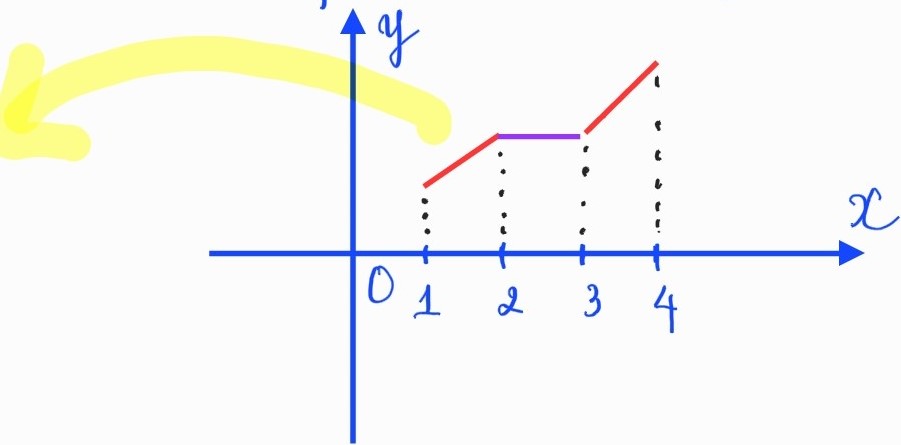
Thế nhưng chúng ta hãy để ý thêm rằng nếu \(f^\prime (x) =0, \forall x \in [a;b] \Rightarrow f(x) \) hàm hằng trên \([a;b]\)
Xét bài tập sau:
Cho hàm số \(y=f(x)\) có đạo hàm \(f^\prime (x) \geq 0, \forall x \in (1;4)\) và \(f^\prime (x) = 0 , \forall x \in [2;3] \).
Mệnh đề nào dưới đây là sai?
A. Hàm số \(f(x)\) đồng biến trên \((1;2)\)
B. Hàm số đồng biến trên \([3;4]\)
C. \(f(\sqrt{5})=f(\sqrt{7})\)
D. Hàm số đồng biến trên \((1;4)\)
Hướng dẫn giải



Cho em hỏi về lý thuyết về phần đơn điệu ạ. Mong Thầy trả lời giúp em ạ,
Em có biết tới định lý sau: “Nếu hàm số f đồng biến trên K thì SUY RA f’>=0 trên K”. Vậy thì trong những trường hợp nào thì f’=0 được ạ. Thầy có thể cho em 1 VD được không?
Chào Khang, cảm ơn em vì câu hỏi, một ví dụ đơn giản dễ thấy nhất đó là hàm số \(y=x^3\) là hàm số đồng biến trên \(\mathbb{R}\) và có đạo hàm \(y^ \prime = 3x^2 \geq 0\) đó em.