Bài viết sẽ nói về tỉ số thể tích trong việc tính thể tích khối đa diện ở lớp 12. Đây là bài mình muốn chia sẻ từ lâu rồi, nay gặp đề thi THPT 2020 câu 47 (mã đề 101) thấy ý tưởng này có thể sử dụng nên quyết định xúc luôn.
Chuyện là thế này. Khi nói về tỉ số thể tích, ngoài ba cái tỉ số thể tích trong khối chóp, lăng trụ, chắc cũng ít bạn để ý rằng:
Tỉ số thể tích = lập phương tỉ số đồng dạng
Và cũng không quên nhắc thêm rằng, tỉ số diện tích = bình phương tỉ số đồng dạng
“Đồng dạng” ở đây, nói cho bài bản thì lâu lắm, nên bài viết chỉ chia sẻ kinh nghiệm ngắn gọn là hai cái hình giống hệt nhau về hình dạng, chỉ là phóng to hay thu nhỏ lại thôi; và quan trọng nhất là nó liên quan đến sự kiện “song song” (bản chất là phép vị tự). Hãy xem ví dụ sau nhé.
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm SA, SB, SC, SD. Khi đó, tỉ số $\dfrac{{{V}_{S.MNPQ}}}{{{V}_{S.ABCD}}}$ là:
A. $\dfrac{1}{4}$ B. $\dfrac{1}{8}$
C. $\dfrac{1}{16}$ D. $\dfrac{1}{64}$
Phân tích–giải: Ở bài này chúng ta có nhiều cách để xử lý: Chẳng hạn dùng công thức tỉ số thể tích chóp tứ giác, ở bài viết này, ta có: $\dfrac{{{V}_{S.MNPQ}}}{{{V}_{S.ABCD}}}=\dfrac{\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}}{4}\left( 2+2+2+2 \right)=\dfrac{1}{8}$ hoặc chia khối chóp thành 2 khối chóp tam giác sau đó dùng tỉ số thể tích cho nó bài bản như “Sách giáo khoa”.
Tuy nhiên, nếu linh hoạt một chút, các bạn sẽ thấy ngay do (MNPQ) // (ABCD), nên nhìn một cách “thoải mái” chút là S.MNPQ đồng dạng với S.ABCD, với tỉ số đồng dạng chính là tỉ số mấy cạnh $k=\dfrac{SM}{SA}=\dfrac{SN}{SB}=\dfrac{SP}{SC}=\dfrac{SQ}{SD}=\dfrac{1}{2}$, và do đó, có ngay kết quả
$\dfrac{{{V}_{S.MNPQ}}}{{{V}_{S.ABCD}}}={{\left( \dfrac{1}{2} \right)}^{3}}=\dfrac{1}{8}$
Chọn B.
Bây giờ, bạn đã hiểu ý tui rồi phải không nào, tui thêm một ví dụ nữa để các bạn thấy nó mạnh cỡ nào trước khi vào câu 47 của đề thi THPT 2020 nhé.
Ví dụ 2. Cho khối chóp $S.ABCD$ có đáy là hình bình hành $ABCD$. Gọi $M$, $N$, $P$, $Q$ lần lượt là trọng tâm các tam giác $SAB$, $SBC$, $SCD$, $SDA$. Biết thể tích khối chóp $S.MNPQ$ là $V$, khi đó thể tích của khối chóp $S.ABCD$ là:
A. $\dfrac{27V}{4}$. B. ${{\left( \dfrac{9}{2} \right)}^{2}}V$.
C. $\dfrac{9V}{4}$. D. $\dfrac{81V}{8}$.
Phân tích–giải.
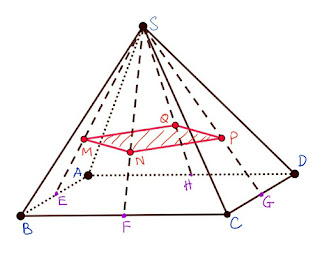
Do sự kiện “song song” chúng ta có tứ giác MNPQ đồng dạng với tứ giác EFGH (thực ra đây là một phép vị tự tâm S, tỉ số 2/3 biến EFGH thành MNPQ)
Cho nên dễ thấy chóp S.MNPQ đồng dạng với S.EFGH theo tỉ số $\dfrac{SM}{SE}=\dfrac{SN}{SF}=\dfrac{SP}{SG}=\dfrac{SQ}{SH}=\dfrac{2}{3}$. Chúng ta có ngay:
$\dfrac{{{V}_{S.MNPQ}}}{{{V}_{S.EFGH}}}={{\left( \dfrac{2}{3} \right)}^{3}}=\dfrac{8}{27}$
Hay: ${{V}_{S.MNPQ}}=\dfrac{8}{27}{{V}_{S.EFGH}}$ (1)
Mặt khác ${{V}_{S.EFGH}}=\dfrac{1}{2}{{V}_{S.ABCD}}$ (2) (do ${{S}_{EFGH}}=\dfrac{1}{2}{{S}_{ABCD}}$)
Từ (1) và (2) ta có: ${{V}_{S.MNPQ}}=\dfrac{8}{27}.\dfrac{1}{2}{{V}_{S.ABCD}}=\dfrac{4}{27}{{V}_{S.ABCD}}$
Vậy, ${{V}_{S.ABCD}}=\dfrac{27}{4}{{V}_{S.MNPQ}}=\dfrac{27}{4}V$. Chọn phương án A.
–––––––
Bây giờ, chúng ta cùng xem một bài toán trong đề thi THPT 2020 nhé.
ĐỀ BÀI: Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên bằng $2a$ và $O$ là tâm của đáy. Gọi $M$,$N$, $P$, $Q$ lần lượt là các điểm đối xứng với $O$ qua trọng tâm của các tam giác $SAB$, $SBC$, $SCD$, $SDA$ và ${S}’$ là điểm đối xứng với $S$ qua $O$. Thể tích của khối chóp $S’.MNPQ$ bằng
A.$\dfrac{20\sqrt{14}{{a}^{3}}}{81}$. B.$\dfrac{40\sqrt{14}{{a}^{3}}}{81}$.
C.$\dfrac{10\sqrt{14}{{a}^{3}}}{81}$. D.$\dfrac{2\sqrt{14}{{a}^{3}}}{9}$.
Phân tích–lời giải
Để dễ diễn đạt, ta gọi E, F, G, H lần lượt là trọng tâm tam giác SAB, SBC, SCD, SDA. Và X, Y, Z, T lần lượt trung điểm AB, BC, CD, DA (để vẽ trọng tâm ý mà)
Gọi I là giao điểm EG và FH, J là giao điểm MP và NQ, tất nhiên I, J này cũng nằm trên SO luôn (Chúng ta đang làm trắc nghiệm mà, đừng quá câu nệ việc chứng minh đồng quy héng, nó sờ sờ ra đó cả mà)
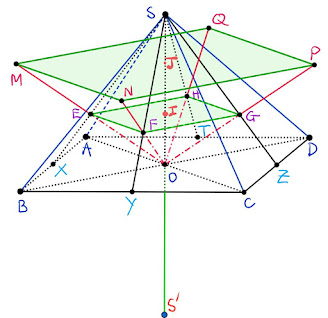
Lúc này nó hơi bị giống Ví dụ 2, rồi đó, chiến thôi:
Khúc đầu quan trọng nè, xét tam giác OPJ, thấy ngay IG // PJ, mà G trung điểm OP nên I là trung điểm OJ.
Xét tam giác SOZ, ta có: IG // OZ thế nên: $\dfrac{SI}{SO}=\dfrac{SG}{SZ}=\dfrac{2}{3}$, suy ra $OI=\dfrac{1}{2}SI$. Vậy là ta có: OI = IJ = JS luôn (chia 3 khúc bằng nhau), suy ra \[OJ=\dfrac{2}{3}OS=\dfrac{2}{3}O{S}’\] hay ${S}’J=\dfrac{5}{2}OJ$
Vậy, ta có:
${{V}_{{S}’.MNPQ}}=\dfrac{5}{2}{{V}_{O.MNPQ}}$(1)
Bây giờ, do sự kiện “song song” chúng ta có chóp O.EFGH đồng dạng với chóp O.MNPQ theo tỉ số $k=\dfrac{OE}{OM}=\dfrac{OF}{ON}=\dfrac{OG}{OP}=\dfrac{OH}{OQ}=\dfrac{1}{2}$ (vì đối xứng mà) $\Rightarrow {{V}_{O.EFGH}}={{\left( \dfrac{1}{2} \right)}^{3}}{{V}_{O.MNPQ}}$
Nên ${{V}_{O.MNPQ}}=8{{V}_{O.EFGH}}$ (2)
Cũng theo ở trên chúng ta đã biết $OI=\dfrac{1}{2}SI$, do đó ${{V}_{O.EFGH}}=\dfrac{1}{2}{{V}_{S.EFGH}}$ (3)
Tiếp tục nà, tương tự Ví dụ 2 ở trên, ta có ngay: S.EFGH đồng dạng S.XYZT theo tỉ số $\dfrac{SE}{SX}=\dfrac{SF}{SY}=\dfrac{SG}{SZ}=\dfrac{SH}{ST}=\dfrac{2}{3}$, cho nên ta có: ${{V}_{S.EFGH}}={{\left( \dfrac{2}{3} \right)}^{3}}{{V}_{S.XYZT}}=\dfrac{8}{27}{{V}_{S.XYZT}}$ (4)
Mà: ${{V}_{S.XYZT}}=\dfrac{1}{2}{{V}_{S.ABCD}}$ (5)
Vậy, từ (1), (2), (3), (4), (5) nối lại thôi, ta có: ${{V}_{{S}’.MNPQ}}=\dfrac{5}{2}.8.\dfrac{1}{2}.\dfrac{8}{27}.\dfrac{1}{2}{{V}_{S.ABCD}}=\dfrac{40}{27}{{V}_{S.ABCD}}$
Mặt khác, việc tính ${{V}_{S.ABCD}}$quá dễ dàng đúng không nè, ta có: $SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\sqrt{{{\left( 2a \right)}^{2}}-{{\left( \dfrac{a\sqrt{2}}{2} \right)}^{2}}}=\dfrac{a\sqrt{14}}{2}$, và ${{V}_{S.ABCD}}=\dfrac{1}{3}.SO.{{S}_{ABCD}}=\dfrac{1}{3}.\dfrac{a\sqrt{14}}{2}.{{a}^{2}}=\dfrac{\sqrt{14}}{6}{{a}^{3}}$
Vậy: ${{V}_{{S}’.MNPQ}}=\dfrac{20\sqrt{14}}{81}{{a}^{3}}$. Chọn phương án A.
Lời bình. Bài này bài giải nhìn có vẻ dài dòng để đọc giả dễ hiểu ý tưởng, chứ khi hiểu ý tưởng, bỏ qua việc trình bày (dùng cho trắc nghiệm) thì rất nhanh đấy. Tất nhiên bài này có nhiều cách giải, ở đây tôi không nhắc lại một số cách đã có trên Internet, và đây là sản phẩm tôi nghĩ ra chứ không sao chép bất kì nguồn nào
Thay lời kết
Thực ra những thứ mà ta nói “đồng dạng” ở trên, chẳng qua chính là nhờ phép vị tự, đây có thể xem là một đề tài mở rộng cho bạn đọc trong việc sử dụng phép vị tự giải quyết một số bài thể tích, có thể ý tưởng của tác giả trong bài toán này là kết hợp phép đối xứng và vị tự. Từ đây GV có thể “chế ra” một loạt bài thú vị nữa đấy.
Chúc bạn đọc thành công.