Đây là bộ đề thi giữa học kì I Toán 10 theo chương trình mới năm học 2022-2023 của một số trường, mời các bạn tham khảo nhé
ĐỀ 1: BÀ ĐIỂM (15 PHÚT).
Bài 1: (3,0 điểm). Cho tập hợp \(A = \left\{ {x \in \mathbb{Z}\mid \left( {2{x^2} – 5x + 2} \right)\left( { – {x^2} + x + 6} \right) = 0} \right\}\) và tập hợp \(B = \left\{ {\dfrac{{n – 2}}{{n + 1}}\mid n \in \mathbb{N},n \le 5} \right\}\). Liệt kê các phần tử của tập hợp A và tập hợp \({\rm{B}}\).
Bài 2: (4,0 điểm) Cho \(A = \left( { – \infty ;2} \right),B = \left[ {1;7} \right)\). Tìm \(A \cap B;A \cup B;A \setminus B;{C_\mathbb{R}}A\)
Bài 3: (3,0 điểm) Một công ty dự định chi không quá 900 triệu đồng để quảng cáo trên truyền hình. Biết giá quảng cáo ở khung giờ 20h00 – 21h00 là 30 triệu đồng cho 15 giây/1 lần quảng cáo. Giá quảng cáo vào khung giờ từ \(17{\rm{\;h}}00\) – 18h00 là 6 triệu đồng cho 15 giây/1 lần quảng cáo. Công ty yêu cầu quảng cáo về số lần phát như sau: có ít nhất 10 lần quảng cáo vào khung giờ từ \(20{\rm{\;h}}00\) – 21h00 và không quá 50 lần quảng cáo vào khung giờ từ \(17h00 – 18\) h00. Hãy tìm phương án phát mỗi loại quảng cáo để công ty có thể phát được số lần quảng cáo nhiều nhất.
ĐỀ 2: AN LẠC.
Bài 1: (1,0 điểm).
a) Lập mệnh đề phủ định của các mệnh đề sau:
A: ” \(\forall n \in \mathbb{N}, n(n+1)\) chia hết cho 2 “
B: ” \( \forall x \in \mathbb{R}, x^2 \leq x \)”
b) Xét tính đúng sai của các mệnh đề sau:
C:” Nếu tứ giác \(ABCD\) là hình bình hành thì tứ giác \(ABCD\) có hai đường chéo cắt nhau tại trung điểm mỗi đường”
D: “Hai đường thẳng \(y = 2x + 1\) và \(y = – 2x + 1\) song song với nhau”.
Bài 2: (2,0 điểm) Xác định các tập hợp sau bằng cách liệt kê:
a) \(A = \left\{ {x \in \mathbb{R}\mid {x^2} – 5x + 6 = 0} \right\}\)
b) \(B = \{ x \in \mathbb{Z}\mid – 4 < x \le 3\} \)
c) \(C = \left\{ {x \in \mathbb{Q}\mid \left( {2{x^2} – 3x + 1} \right)\left( {{x^2} – 2} \right) = 0} \right\}\)
d) \(D = \{ x \in \mathbb{N}||2x – 3\mid \le 5\} \)
Bài 3: (2,0 điểm) Xác định các tập hợp sau:
a) \(\left[ { – 4;5\left] \cap \right[1;6} \right]\)
b) \(\left( { – 4;2} \right] \cup \left( { – \infty ;0} \right]\)
c) \(\left( { – 5;2} \right) \setminus \left[ {1;3} \right)\)
d) \(\mathbb{R} \setminus \left( { – \infty ;5} \right]\)
Bài 4: (1,0 điểm) Trong kì thi chọn học sinh giỏi các môn văn hoá, lớp 10A có 8 học sinh đăng kí thi môn Toán, 6 học sinh đăng kí thi môn Vật Lý, 7 học sinh đăng kí thi môn Hoá Học, trong đó 4 học sinh đăng kí thi cả Toán và Vật Lý, 5 học sinh đăng kí thi cả Toán và Hoá Học, 3 học sinh đăng kí thi cả Vật Lý và Hoá học, 2 học sinh đăng kí thi cả ba môn. Hỏi lớp 10A có tất cả bao nhiêu học sinh đăng kí thi học sinh giỏi các môn Toán, Vật Lý, Hoá học.
Bài 5: (1,0 điểm) Cho \({\rm{sin}}x = \dfrac{3}{5}\) với \({90^ \circ } < x < {180^ \circ }\). Tính \({\rm{cos}}x,{\rm{tan}}x,{\rm{cot}}x,3{\rm{co}}{{\rm{s}}^2}x + 5{\rm{ta}}{{\rm{n}}^2}x\)
Bài 6: (1,0 điểm) Cho tam giác \(ABC\) biết \(AB = 6{\rm{\;cm}},BC = 8{\rm{\;cm}},\widehat {ABC} = {60^ \circ }\)
a) Tính độ dài cạnh \(AC\) và diện tích tam giác \(ABC\).
b) Tính độ dài đường cao \(AH\) của tam giác \(ABC\).
Bài 7: (1,0 điểm) Cho tam giác \(ABC\). Chứng minh các đẳng thức sau:
a) \({\rm{cos}}\left( {\dfrac{{B + C}}{2}} \right) = {\rm{sin}}\dfrac{A}{2}\)
b) \({\rm{tan}}A + {\rm{tan}}\left( {B + C} \right) = 0{\rm{\;}}\left( {A \ne {{90}^ \circ }} \right)\)
ĐỀ 3: BÀ ĐIỂM.
Bài 1: \((3,0\) điểm). Tìm tập xác định các hàm số sau:
a) \(y = \dfrac{{x – 2}}{{{x^2} – 5x + 6}}\).
b) \(y = \dfrac{{\left| {x + 3} \right| + 2}}{{\sqrt {3 – x} + 2}}\)
c) \(y = \dfrac{{\sqrt {4 – x} + \sqrt {4 + x} }}{{ – {x^2} – 3x + 4}}\)
Bài 2: (1,5 điểm) Xác định công thức hàm số bậc hai có đồ thị như hình vẽ:
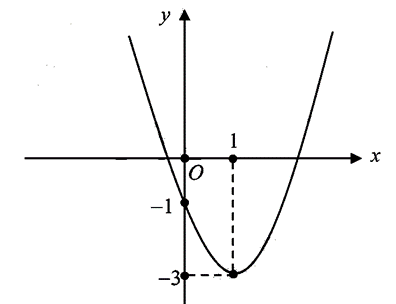
Bài 3: (1,5 điểm) Cho hàm số \(y = \left( {1 – m} \right){x^2} + 4\left( {m – 1} \right)x + {m^2} – 9m + 3{\rm{\;}}(1 – m \ne 0,m\) là tham số). Tìm tất cả các giá trị \(m\) sao cho hàm số đạt giá trị lớn nhất bằng 5 .
Bài 4: (1,5 điểm) Cho \({\rm{sin}}x = \dfrac{2}{3}\left( {{{90}^ \circ } < x < {{180}^ \circ }} \right)\). Tính \({\rm{cos}}x,{\rm{tan}}x,{\rm{cot}}x\).
Bài 5: \((2,0\) điểm) Trường THPT Bà Điểm sắp khánh thành, để trang trí các bồn hoa góc sân trường, nhà trường mua hàng rào gỗ có chiều dài \(4m\) sau đó cắt thành 2 phần. Phần thứ nhất uốn thành hình vuông và phần thứ hai uốn thành hình tròn. Hãy cho biết phương án cắt sao cho tổng diện tích hai hình thu được chiếm diện tích nhỏ nhất.

ĐỀ 4: BÌNH HƯNG HÒA
Bài 1: (1,0 điểm). Xét tính đúng, sai của mệnh đề sau và viết mệnh đề phủ định .
Bài 2: (1,0 điểm) Cho \(A = \{ x \in \mathbb{Z}\mid – 2 \le x < 4\} \) và \(B = \left\{ {n \in \mathbb{N}\mid n \le 5} \right\}\). Viết tập hợp \({\rm{A}}\) và \({\rm{B}}\) dưới dạng liệt kê các phần tử. Xác định các tập hợp \(A \cup B,A \setminus B\).
Bài 3: (2,0 điểm) Cho hai tập hợp \(A = \left\{ {x \in \mathbb{R}\mid – 1 \le x \le 4} \right\}\) và \(B = \{ x \in \mathbb{R}\mid x < 0\} \).
a) Dùng kí hiệu đoạn, khoảng, nửa khoảng để viết các tập hợp \(A,B\).
b) Xác định các tập hợp \(A \cap B,A \cup B,A \setminus B,{C_\mathbb{R}}B\).
Bài 4: \((2,0\) điểm) Biểu diễn miền nghiệm của bất phương trình \(3x + y – 3 > 0\) trên mặt phẳng toạ độ \(Oxy\)
Bài 5: (2,0 điểm) Cho tam giác \(ABC\) có . Giải tam giác và tính diên tích của tam giác \(ABC\) (Các kết quả làm tròn đến chữ số thập phân thứ hai)
Bài 6: (1,0 điểm) Bác Hai cần trồng khoai và ngô trên một mảnh đất có diện tích 6ha. Nếu trồng 1ha khoai thì cần 40 ngày công và thu được 50 triệu đồng. Nếu trồng 1ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Bác Hai cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng bác Hai chỉ có thể sử dụng không quá 160 ngày công cho việc trồng khoai và ngô.
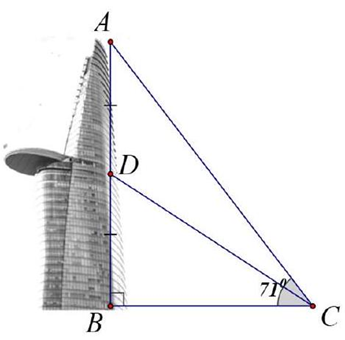
Bài 7: (1,0 điểm) Muốn đo chiều cao của một toà nhà, bạn Nam chọn hai điểm \(B\) và \(C\) trên mặt đất có khoảng cách \(BC = 185{\rm{\;m}}\). Gọi \(A\) là đỉnh toà nhà và \(D\) là trung điểm của đoạn thẳng \(AB\). Biết rằng \({\rm{cos}}\widehat {ACD} = \dfrac{{2\sqrt 2 }}{3}\). Tính chiều cao \(AB\) của toà nhà.
ĐỀ 5: ĐÀO SƠN TÂY
Bài 1: \((1,0\) điểm). Xét tính đúng, sai của mệnh đề sau và viết mệnh đề phủ định:
Bài 2: (1,0 điểm) Cho các tập hợp \(A = \left\{ {0;2;5} \right\};B = \left\{ { – 3; – 2; – 1;0;1;2;3} \right\}\). Xác định các tập hợp \(A \cup B;A \setminus B\).
Bài 3: (1,0 điểm) Cho tập hợp \(C = \left\{ {2,4,6} \right\}\). Liệt kê tất cả các tập hợp con của tập hợp \(C\).
Bài 4: \({\rm{\;}}(2,0\) điểm) Xác định các tập hợp sau và biểu diễn trên trục số
a) \(\left[ { – 3;5} \right) \cap \left[ { – 1;7} \right]\)
b) \(\left[ { – \dfrac{1}{2}; + \infty } \right) \setminus \left[ { – 4;\dfrac{3}{2}} \right]\).
Bài 5: (1,0 điểm) Mỗi học sinh lớp 10A đều biết chơi cờ tướng hoặc cờ vua, biết rằng có 25 em biết chơi cờ tướng, 30 em biết chơi cờ vua và 15 em biết chơi cả hai. Hỏi lớp \(10{\rm{\;A}}\) có sĩ số lớp là bao nhiêu học sinh?
Bài 6: (1,0 điểm) Biểu diễn miền nghiệm của bất phương trình sau: \(x + 2y – 4 \ge 0\)
Bài 7: (1,5 điểm) Cho tam giác \(MNP\) có \(MN = 10,MP = 8\) và góc \(NMP = {120^ \circ }\)
a) Tính cạnh \(NP\) và tính bán kính đường tròn ngoại tiếp tam giác \(MNP\).
b) Tính diện tích tam giác \(MNP\).
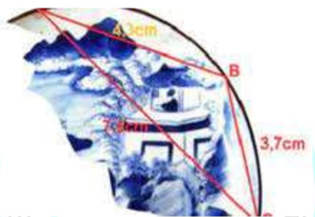
Bài 8: \((0,5\) điểm) Khi khai quật một ngôi mộ cổ người ta tìm được một mảnh của một chiếc đĩa phẳng hình tròn bị vỡ. Dựa vào các tài liệu đã có, các nhà khảo cổ đã biết hình vẽ trên phần còn lại của chiếc đĩa. Họ muốn làm một chiếc đĩa mới phỏng theo chiếc đĩa này. Em hãy giúp họ tìm bán kính chiếc đĩa biết \(AB = 4,3{\rm{\;cm}},AC = 7,5{\rm{\;cm}},BC = 3,7{\rm{\;cm}}\)
ĐỀ 6: DIÊN HỒNG
Bài 1: \((2,0\) điềm) Biểu diễn miền nghiệm của bất phương trinnh và hệ bất phương trình sau trên mặt phẳng tọa độ:
a) \(x + 2y – 8 \le 0\)
b) \(\left\{ {\begin{array}{*{20}{l}}{x + y \le 2}\\{y – x \le 2}\\{y > – 1}\end{array}} \right.\).
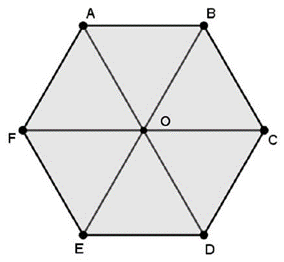
Bài 2: \((1,5\) điềm) Cho lục giác đều \({\rm{ABCDEF}}\) có tâm \({\rm{O}}\). Xét các vectơ có hai điềm đầu mút lấy từ các điểm \({\rm{O}},{\rm{A}},{\rm{B}},{\rm{C}},{\rm{D}},{\rm{E}},{\rm{F}}\).
a) Hãy chỉ ra các vectơ khác \(\vec 0\) và cùng phương với vectơ \(\overrightarrow {OA} \).
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).
Bài 3: (1,0 điểm) Cho tam giác \(ABC\) có Tính độ dài các cạnh \(a,b\).
Bài 4: (1,5 điểm) Cho 6 điểm \({\rm{A}},{\rm{B}},{\rm{C}},{\rm{D}},{\rm{E}},{\rm{F}}\). Chứng minh đẳng thức: \(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow {AE} + \overrightarrow {BF} + \overrightarrow {CD} \).
Bài 5: (2,0 điểm) Một hợp tác xã chăn nuôi dự đinh trộn hai loại thức ăn gia súc \(X\) Và \(X\) để tạo thành thức ăn hỗn hợp cho gia súc. Giá một bao loại \(X\) là 250 nghìn đồng, giá một bao loại \(Y\) là 200 nghìn đồng. Mỗi bao loại \(X\) chứa 2 đơn vị chất dinh dưỡng \(A,2\) đơn vi chất dinh dưỡng \(B\) và 2 đơn vi chất dinh dưỡng \(C\). Mỗi bao loại \(Y\) chưa 1 đơn vị chất dinh dưỡng \(A,9\) đơn vị chất dinh dưỡng \(B\) và 3 đơn vi chất dính dưỡng \(C\). Tìm chi phí nhỏ nhất để mua hai loại thức ăn gia súc \(X\) và \(Y\) sao cho hỗn hợp thu được chứa tối thiểu 12 đơn vị chất dinh dưỡng \(A,36\) đơn vị chất dinh dưỡng \(B\) và 24 đơn vị chất dinh dưỡng \(C\).
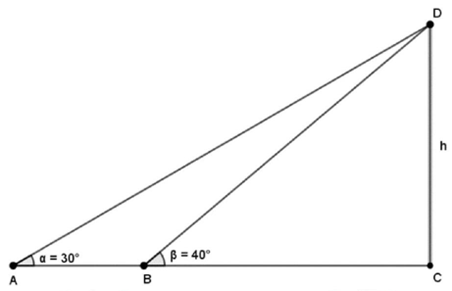
Bài 6: \({\rm{\;}}(2,0\) điểm \()\) Để đo chiều cao của một tòa nhà, người ta chọn 2 điểm \({\rm{A}}\) và \({\rm{B}}\) thẳng hàng với chân \({\rm{C}}\) của tòa nhà, cách nhau \(15{\rm{\;m}}\). Sử dụng giác kế, từ \({\rm{A}}\) và \({\rm{B}}\) tương ứng nhìn thấy đỉnh \({\rm{D}}\) của tòa nhà dưới các góc \({35^ \circ }\) và \({40^ \circ }\) so với phương nằm ngang. Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét?
ĐỀ 7: HÀN THUYÊN
PHẦN TRẮC NGHIỆM (5,0 điểm)
Câu 1. Cho tam giác \(ABC\) có \(BC = 5\) và \(\hat A = {45^ \circ }\). Bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\) bằng?
A. \(5\sqrt 2 \).
B. \(\dfrac{{5\sqrt 2 }}{2}\).
C. 10 .
D. \(10\sqrt 2 \).
Câu 2. Cho tập hợp \(A = \left\{ {x \in \mathbb{R}\mid x\left( {x + 1} \right) > {x^2}} \right\}\). Hãy xác định tập hợp A
A. \(A = \left( { – \infty ; + \infty } \right)\).
B. \(A = \left( { – 2; + \infty } \right)\).
C. \(A = \left( { – \infty ;0} \right)\).
D. \(A = \left( {0; + \infty } \right)\).
Câu 3. Một học sinh dự định làm các bình hoa bằng giấy để bán trong một hội chợ gây quỹ từ thiện. Cần 1 giờ để làm bình hoa loại nhỏ và bán với giá 100 nghìn đồng, 90 phút để làm bình hoa loại lớn bán với giá 200 nghìn đồng. Học sinh này chỉ thu xếp được tối đa 1 ngày nghỉ để làm và ban tổ chức yêu cầu phải làm ít nhất là 12 bình hoa. Gọi \(x,y\) lần lượt là số bình hoa loại nhỏ và số bình hoa loại lớn mà bạn đó làm được. Tìm hệ bất phương trình thoả theo yêu cầu trên.
A. \(\left\{ {\begin{array}{*{20}{l}}{x + y \ge 12}\\{x + 1,5y \ge 24}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\)
B. \(\left\{ {\begin{array}{*{20}{l}}{x + y \ge 12}\\{x + 1,5y \le 24}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\)
C. \(\left\{ {\begin{array}{*{20}{l}}{x + y \ge 12}\\{x + 1,5y \le 1}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\)
D. \(\left\{ {\begin{array}{*{20}{l}}{x + y \ge 12}\\{1,5x + y \le 24}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\)
Câu 4. Cho hai tập hợp \(A = \left\{ {1;3;6} \right\}\) và \(B = \left\{ {0;1;3;6} \right\}\). Khẳng định nào sau đây đúng?
A. \(A \in B\).
B. \(A \subset B\).
C. \(A = B\).
D. \(B \subset A\).
Câu 5. Cho tập hợp \(X = \left( { – \infty ;5} \right] \cap \left( { – 8; + \infty } \right)\). Khẳng định nào sau đây đúng?
A. \(X = \left( { – 8;5} \right]\).
B. \(X = \left( { – \infty ;5} \right]\).
C. \(X = \left( { – \infty ; + \infty } \right)\).
D. \(X = \left( { – 8; + \infty } \right)\).
Câu 6. Trong các tập hợp sau, tập hợp nào là tập rỗng?
A. \(F = \left\{ {x \in \mathbb{Z}\mid {x^2} = 0} \right\}\).
B. \(M = \left\{ {x \in \mathbb{N}\mid 2x – 1 = 0} \right\}\).
C. \(E = \left\{ {x \in \mathbb{R}\mid {x^2} – 6x + 9 = 0} \right\}\).
D. \(N = \left\{ {x \in \mathbb{Q}\mid 3x + 2 = 0} \right\}\).
Câu 7. Trong các đẳng thức sau, đẳng thức nào sai?
A. \({\rm{sin}}\left( {{{180}^ \circ } – \alpha } \right) = {\rm{sin}}\alpha \).
B. \({\rm{cos}}\left( {{{90}^ \circ } – \alpha } \right) = {\rm{sin}}\alpha \)
C. \({\rm{sin}}\left( {{{90}^ \circ } – \alpha } \right) = {\rm{cos}}\alpha \)
D. \({\rm{cos}}\left( {{{180}^ \circ } – \alpha } \right) = {\rm{sin}}\alpha \)
Câu 8. Cho tam giác \(ABC\), gọi \(AB = c,AC = b,BC = a\). Hãy chộn khẳng định đúng
A. \(\dfrac{a}{{{\rm{sin}}a}} = \dfrac{b}{{{\rm{sin}}b}} = \dfrac{c}{{{\rm{sin}}c}} = R\).
B. \(S_{\triangle A B C}=\dfrac{a b c}{4 \mathrm{R}} \).
C. (S_{\triangle A B C}=\dfrac{a+b+c}{4 \mathrm{R}}).
D. \(\dfrac{a}{{{\rm{cos}}a}} = \dfrac{b}{{{\rm{cos}}b}} = \dfrac{c}{{{\rm{cos}}c}} = R\).
Câu 9. Sử dụng kí hiệu khoảng, đoạn để viết tập hợp \(A = \{ x \in \mathbb{R}\mid 3 < x \le 10\} \)
A. \(A = \left( {3;10} \right]\).
B. \(A = \left( {3;10} \right)\).
C. \(A = \left[ {3;10} \right]\).
D. \(A = \left[ {3;10} \right)\).
Câu 10. Cho các tập hợp \(A = \left[ { – 5;2} \right)\) và \(B = \left( { – \infty ;1} \right)\). Tìm tập hợp \(A \cup B\)
A. \(A \cup B = \left( { – \infty ;1} \right)\).
B. \(A \cup B = \left[ { – 5; + \infty } \right)\).
C. \(A \cup B = \left[ { – 5;1} \right)\).
D. \(A \cup B = \left( { – \infty ;2} \right)\).
Câu 11. Cho tập hợp \(X = \left\{ {1;4;5} \right\}\). Số tập hợp con có hai phân tử của \(X\) là
A. 4 .
B. 3 .
C. 5 .
D. 8 .
Câu 12. Cho tam giác \(ABC\) có ba cạnh \(a = 5,b = 6,c = 7\). Tính \({\rm{cos}}A\)
A. \(\dfrac{{55}}{{42}}\).
B. \(\dfrac{{10}}{7}\).
C. \(\dfrac{5}{7}\).
D. \(\dfrac{2}{{21}}\).
Câu 13. Cho tam giác \(ABC\), gọi \(AB = c,AC = b,BC = a\). Đẳng thức nào sau đây sai?
A. \({b^2} = {a^2} + {c^2} – 2ac{\rm{cos}}C\).
B. \({b^2} = {a^2} + {c^2} – 2ac{\rm{cos}}B\).
C. \({c^2} = {a^2} + {b^2} – 2ab{\rm{cos}}C\).
D. \({a^2} = {b^2} + {c^2} – 2bc{\rm{cos}}A\).
Câu 14. Hãy liệt kê các phân tử của tập hợp \(X = \left\{ {x \in \mathbb{Z}\mid {x^2} + 2x – 3 = 0} \right\}\)
A. \(X = \left\{ { – 3} \right\}\).
B. \(X = 1\).
C. \(X = \left\{ { – 3;1} \right\}\).
D. \(X = \left\{ 1 \right\}\).
Câu 15. Cho tập hợp \(A = \left\{ {1;3;4} \right\}\). Hỏi tập \(A\) có bao nhiêu phần tử
A. 3 phần tử.
B. Vô số phần tử.
C. 4 phần tử.
D. 2 phần tử.
Câu 16. Cho hai tập hợp \(A = \left[ {1;4} \right)\) và \(B = \left[ {2;8} \right)\). Tìm \(A \setminus B\)
A. \(A \setminus B = \left[ {1;8} \right]\).
B. \(A \setminus B = \left[ {1;2} \right)\).
C. \(A \setminus B = \left[ {4;8} \right]\).
D. \(A \setminus B = \left[ {2;4} \right)\).
Câu 17. Hình vẽ sau đây là biểu diễn trên trục số của tập hợp nào dưới đây?

A. \(\left( { – 2;1} \right)\).
B. \(\left[ { – 2;1} \right]\).
C. \(\left( { – 2;1} \right]\).
D. \(\left[ { – 2;1} \right)\).
Câu 18. Cho tam giác \(ABC\) có \(\hat B = {60^ \circ },AB = 10,BC = 6\). Tính độ dài cạnh \(AC\)
A. 14 .
B. \(2\sqrt {19} \).
C. 76 .
D. \(6\sqrt 2 \).
Câu 19. Cho hai tập hợp \(A = \left\{ {1;2;4;6} \right\}\) và \(B = \left\{ {1;2;3;4;5;6;7;8} \right\}\). Khi đó tập \({C_B}A\) là
A. \(\left\{ {2;6;7;8} \right\}\).
B. \(\left\{ {3;5;7;8} \right\}\).
C. \(\left\{ {4;6} \right\}\).
D. \(\left\{ {1;2;4;6} \right\}\).
Câu 20. Lớp \(10A\) có tất cả 40 họ̣ sinh trong đó có 15 học sinh giỏi môn Toán, 20 học sinh giỏi môn Tiếng Anh. Trong đó có 10 học sinh giỏi cả hai môn Toán và môn Tiếng Anh. Hỏi lớp \(10{\rm{\;A}}\) có bao nhiêu học sinh không được khen thưởng, biết rằng muốn được khen thưởng thì bạn đó phải là học sinh giỏi ít nhất một môn Toán hoặc Tiếng Anh.
A. 25 .
B. 15 .
C. 10 .
D. 20 .
PHẦN TỰ LUẬN (5,0 điểm)
Câu 1. (1,0 điểm) Cho \({\rm{tan}}x = 2\). Tính giá trị của biểu thức \(P = \dfrac{{{\rm{sin}}x + 3{\rm{cos}}x}}{{{\rm{cos}}x + 4{\rm{sin}}x}}\).
Câu 2. (1,0 điểm) Tìm tập xác định của hàm số sau \(y = \dfrac{{\sqrt {2x – 1} }}{{{x^2} + 5x – 6}}\).
Câu 3. (2,0 điềm) Cho tam giác \(ABC\) có . Hãy tính
a) Độ dài cạnh \(AC\).
b) Bán kính đường tròn nội tiếp tam giác \(ABC\).
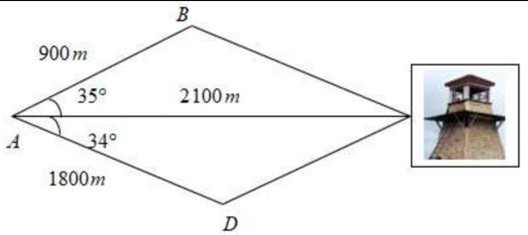
Câu 4. (1,0 điểm) Từ tháp canh \(A\) ta thấy lửa cháy ở \(C\). Biết \(B,D\) là điểm chứa nước chữa cháy (Tham khảo hình vẽ bên dưới). Cho \(AD = 1800{\rm{\;m}},AB = 900{\rm{\;m}},AC = 2100{\rm{\;m}}\), góc \(\widehat {CAB} = {35^ \circ }\) , góc \(\widehat {CA{\rm{D}}} = {34^ \circ }\). Tính khoảng cách từ \(B\) đến \(C\), tính khoảng cách từ \(D\) đến \(C\). Khoảng cách nào lấy được nước chữa cháy gần hơn? (Làm tròn đến hàng đơn vị).
ĐỀ 8: HOÀNG HOA THÁM
Bài 1: (1,5 điểm) Cho mệnh đề \(P:\) “ \(\exists x \in \mathbb{R},{(x – 1)^2} = {(x – 1)^{{\rm{”}}}}\). Viết mệnh đề phủ định của \(P\) và cho biết mệnh đề \(P\) đúng hay sai? Vì sao?
Bài 2: (1,5 điểm) Tìm \(A \cap B,A \cup B,{C_{\rm{R}}}A\) với \(A = \left( { – \infty ;5} \right],B = \left( {5; + \infty } \right)\).
Bài 3: (1,5 điểm) Trên mặt phẳng tọa độ \(Oxy\), biểu diễn miền nghiệm của bất phương trình: \(3x + 2y \le 6\).
Bài 4: (1,5 điểm) Tìm tập xác định của hàm số \(y = \dfrac{{{x^2} – 4}}{{3 – x}} + \sqrt {x + 4} \).
Bài 5: (2,0 điểm) Cho tam giác \(ABC\) có cạnh \(BC = 8,AC = 10,AB = 13\).
a) Tính \({\rm{cos}}A\).
b) Tính diện tích tam giác \(ABC\).
Bài 6: (1,5 điểm) Gia đình bạn An sở hữu một mảnh đất hình tam giác (như hình vẽ). Chiều dài của hàng rào \(MN\) là \(150{\rm{\;m}}\), chiêuu dài của hàng rào \(MP\) là \(230{\rm{\;m}},\widehat {NMP} = {110^ \circ }\).
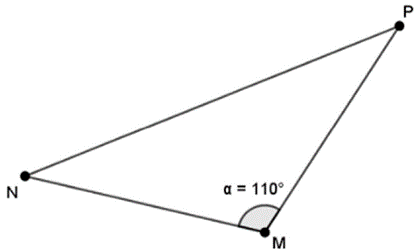
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
b) Chiều dài hàng rào \(NP\) là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
ĐỀ 9: HỒ THI BI
PHẦN TRẮC NGHIỆM (4 điểm)
Câu 1. Trong các mệnh đề sau đay, mệnh đề nào đúng?
A. Số 2021 chia hết cho 5.
B. Số 2020 là số lẻ.
C. Số 2022 chia hết cho 3 .
D. Số 2023 là số chẵn.
Câu 2. Cho tập hợp \(E = \left( {1; + \infty } \right)\). . Tập hợp \({C_\mathbb{R}}E\) là tập hợp nào dưới đây?
A. \(\left( { – \infty ;1} \right]\).
B. \(\left( { – \infty ;1} \right)\).
C. \(\left[ {1; + \infty } \right)\).
D. \(\left\{ 1 \right\}\).
Câu 3. Cho hai tập hợp \(A = \left\{ {1;2;3;4} \right\}\) và \(B = \left\{ {1;3} \right\}\). Phân bù của \(B\) trong \(A\) là
A. \(\emptyset \).
B. \(\left\{ 2 \right\}\).
C. \(\left\{ 4 \right\}\).
D. \(\left\{ {2;4} \right\}\).
Câu 4. Cho hai tập hợp \(A = \left\{ {0;2} \right\}\) và \(B = \left\{ {0;1;2;3} \right\}\). Số tập hợp X thoả mãn \(A \cup X = B\) là
4 .
B. 3 .
C. 1 .
D. 2 .
Câu 5. Xét định lý \(P \Rightarrow Q\). Khẳng định nào dưới đây sai?
A. \(P\) là giả thiết, \(Q\) là kết luận.
B. \(P\) kéo theo \(Q\).
C. \(P\) là điêu kiện cân để có \(Q\).
D. \(P\) là điều kiện đủ để có \(Q\).
Câu 6. Cho tập hợp \(A = \left\{ { – 2;0;1;2} \right\}\). Số phân tử của \(A\) là
A. 1 .
B. 4 .
C. 3 .
D. 2 .
Câu 7. Cho hai tập hợp \(A = \left\{ {0;1;2} \right\}\) và \(B = \left\{ { – 2;0;1} \right\}\). Tập hợp \(A \cap B\) là
A. \(\left\{ { – 2;0;1;2} \right\}\).
B. \(\left\{ { – 2} \right\}\).
C. \(\left\{ {0;1} \right\}\).
D. \(\left\{ 2 \right\}\).
Câu 8. Cho hai tập hợp \(A = \left\{ {0;1;2} \right\}\) và \(B = \left\{ { – 2;0;1} \right\}\). Tập hợp \(A \setminus B\) là
A. \(\left\{ { – 2} \right\}\).
B. \(\left\{ 2 \right\}\).
C. \(\left\{ {0;1} \right\}\).
D. \(\left\{ { – 2;0;1;2} \right\}\).
Câu 9. Cho hai tập hợp \(A = \left\{ {0;1;2} \right\}\) và \(B = \left\{ { – 2;0;1} \right\}\). Tập hợp \(A \cup B\) là
A. \(\left\{ { – 2;0;1;2} \right\}\).
B. \(\left\{ 2 \right\}\).
C. \(\left\{ {0;1} \right\}\).
D. \(\left\{ { – 2} \right\}\).
Câu 10. Cho hai tập hợp \(A = \left\{ { – 1;2} \right\}\) và \(B = \left\{ {x \in \mathbb{R}/{x^2} – 2x = 0} \right\}\). Số phân tử của tập hợp \(A \cup B\) là
A. 4 .
B. 2 .
C. 3 .
D. 1 .
Câu 11. Trong các câu dưới đây, câu nào là mệnh đề?
A. Hôm nay là thứ tư, phải không?
B. Trời hôm nay thật đẹp!
C. Ukraina là một nước thuộc Châu Âu.
D. \({2^{2022}}\) là nột số rất lớn.
Câu 12. Cho tập hợp \(A = \left\{ { – 1;1} \right\}\). Số tập hợp con của \(B\) là
A. 4 .
B. 1 .
C. 2 .
D. 3 .
Câu 13. Cho hai tập hợp \(A = \left( { – \infty ;m + 1} \right)\) và \(B = \left[ {1; + \infty } \right)\). Tìm tất cả các giá trị thực của tham số \(m\) thoả mãn \(A \cap B = \emptyset \)
A. \(m \le 0\).
B. \(m \ge 0\).
C. \(m < 0\).
D. \(m > 0\).
Câu 14. Cho mệnh đề: “Tất cả học sinh lớp 10A1 của trường HỒ THI BI đều biết bơi”. Mệnh đề phủ định của mệnh đề đã cho là
A. Có ít nhật một học sinh lớp 10A1 của trường HỒ THI BI biết bơi.
B. Mọi học sinh lớp 10A1 của trường HỒ THỊ BI đều không biết bơi.
C. Trong các học sinh lớp 10A1 của trường HỒ THỊ BI có bạn không biết bơi.
D. Không có học sinh nào trong lớp 10A1 của trường HỒ THỊ BI biết bơi.
Câu 15. Cho tập hợp \(M = \{ x \in \mathbb{R}/a \le x < b\} \). Mệnh nào dưới đây đúng?
A. \(M = \left[ {a;b} \right)\).
B. \(M = \left( {a;b} \right)\).
C. \(M = \left( {a;b} \right]\).
D. \(M = \left[ {a;b} \right]\).
Câu 16. Tập hợp nào dưới đậy là tập hợp rỗng?
A. \(\left\{ 0 \right\}\).
B. \(\left\{ \emptyset \right\}\).
C. \(\left\{ {x \in \mathbb{R}/{x^2} + 1 = 0} \right\}\).
D. \(\left\{ {x \in \mathbb{R}/2x + 1 = 0} \right\}\).
PHẦN TỰ LUẬN (6 điểm)
Câu 17. (1,0 điểm) Biểu diễn miền nghiệm của bất phương trình \(2x + 3y – 5 < 0\) trên mặt phẳng toạ độ.
Câu 18. (2,0 điểm) Một công ty sãn xuất phân bón dự định sãn xuất hai loại sản phẩm phân bón \(X\) và \(Y\). Các sản phâm này được chế tạo từ hai loại nguyên liệu \(A\) và \(B\). Số tấn dự trữ từng loại nguyên liệu và số tấn từng loại nguyên liệu cần dùng để sản xuất ra 1 tấn sản phẩm được cho trong bảng sau
Gọi \(x,y\) lần lượt là số tấn sãn phẩm \(X\) và \(Y\) mà công ty cần sản xuất.
a) Hãy lập hệ bất phương trình mô tả điều kiện ràng buộc đối với \(x\) và \(y\).
b) Biết rằng khi bán 1 tấn sản phẩm \(X\) lãi được 10 triệu đồng và bán 1 tấn sãn phẩm \(Y\) lãi được 8 triệu đồng. Hãy tìm \(x\) và \(y\) để số tiền lãi mà công ty thu được là lớn nhất.
Câu 19. (2,0 điểm) Cho tam giác \(ABC\) có \(AB = 3,AC = 8\) và
a) Tính độ dài cạnh \(BC\) và diện tích tam giác \(ABC\).
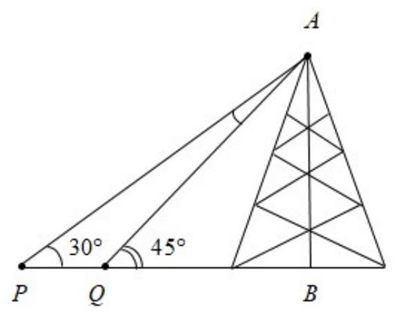
b) Trên cạnh \(AC\) lấy điểm \(M\) sao cho \(BM = 2\sqrt 3 \). Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác \(BCM\). Câu 20. (1,0 điểm) Hai chiếc tàu thuỷ ở hai vị trí \(P\) và \(Q\) cách nhau \(200{\rm{\;m}}\) và thẳng hàng với chân \(B\) của tháp hải đăng \(AB\) trên bờ biển (Tham khảo hình bên dưới). Từ \(P\) và \(Q\), người ta quan sát thấy đỉnh \(A\) của tháp hải đăng \(AB\) dưới các góc \(\widehat {APB} = {30^ \circ }\) và \(\widehat {AQB} = {45^ \circ }\). Tính chiều cao \(AB\) của tháp hải đăng đó. (Kêt quả làm tròn đến một chũu số thập phân).
ĐỀ 10: LẠC HỒNG
Bài 1: (1.0 điểm) Cho mệnh đề .
a) Xét tính đúng sai của mệnh đề \(P\).
b) Phát biểu mệnh đề phủ định của mệnh đề \({\rm{P}}\) và xét tính đúng sai của mệnh đề phủ định đó.
Bài 2: (1.0 điểm) Viết lại các tập hợp sau dưới dạng liệt kê các phân tử:
a) \(A = \{ x \in \mathbb{N}\mid x < 6\} \).
b) \(B = \left\{ {x \in \mathbb{R}\mid {x^2} – 4x + 3 = 0} \right\}\).
Bài 3: (1.0 điểm) Cho \(A = \left\{ {1;2;3;4} \right\}\). Liệt kê các tập con có hai phần tử của tập \(A\).
Bài 4: (1.0 điểm) Cho hai tập hợp \(A = \left( { – 2;5} \right]\) và \(B = \left[ {1;9} \right]\).
a) Tìm \(A \cap B,A \cup B\).
b) Tìm \(A \setminus B,B \setminus A\).
Bài 5: (2.0 điểm) Cho bất phương trình \(x – y – 3 \le 0\).
a) Cặp số \(\left( {1;5} \right)\) có phải là nghiệm của bất phương trình trên không? Vì sao?
b) Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ.
Bài 6: (1.0 điểm) Lớp \(10B\) có 17 học sinh thích môn cầu lông, 18 học sinh thích môn bóng đá. Trong số các học sinh thích môn cầu lông hoặc bóng đá, có 9 học sinh thích cả hai môn cầu lông và bóng đá. Hỏi lớp \(10{\rm{\;B}}\) có tất cả bao nhiêu học sinh? Biết rằng lớp \(10{\rm{\;B}}\) vẫn còn 8 học sinh không thích môn nào (trong hai môn cầu lông và bóng đá).
Bài 7: (1.0 điểm) Cho có \(AB = 5,AC = 8,\hat A = {60^ \circ }\). Tính độ dài cạnh \(BC\). Bài 8: (1.0 điểm) Cho hình bình hành \({\rm{ABCD}}\) tâm \({\rm{O}}\), hãy chỉ ra tất cả các vectơ khác 0
a) Cùng phương với \(\overrightarrow {AD} \).
b) Ngược hướng với \(\overrightarrow {OD} \).
Bài 9: (1.0 điểm) Cho thỏa mãn \({\rm{sin}}B = 2{\rm{sin}}A \cdot {\rm{cos}}C\). Chứng minh: cân.
ĐỀ 11: LÊ HỒNG PHONG
Bài 1: (1,0 điểm) Cho tam giác \(A\) có \(AB = 5,BC = 7,AC = 8\). Tính số đo góc \(A\).
Bài 2: \((1,0\) điểm \()\) Biết \({\rm{sin}}\alpha = \dfrac{2}{3}\left( {{{90}^ \circ } < \alpha < {{180}^ \circ }} \right)\). Hỏi giá trị \({\rm{cot}}\alpha \) là bao nhiêu?
Bài 3: (1,0 điểm) Cho tam giác \(ABC\) có \(AB = 2a,AC = 4a\) và \(\widehat {BAC} = {120^ \circ }\). Tính chiều cao \(AH\) của tam giác \(ABC\).
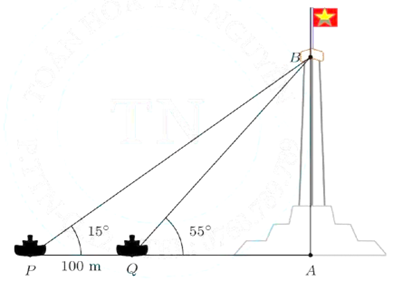
Bài 4: (2,0 điểm) Hai chiếc tàu thủy \(P\) và \(Q\) trên biển cách nhau \(100{\rm{\;m}}\) và thẳng hàng với chân \(A\) của tháp hải đăng \(AB\) ở trên bờ biển. Từ \(P\) và \(Q\) người ta nhìn chiều cao \(AB\) của tháp dưới các góc \(\widehat {BPA} = {15^ \circ }\) và \(\widehat {BQA} = {55^ \circ }\). Tính chiều cao của tháp.
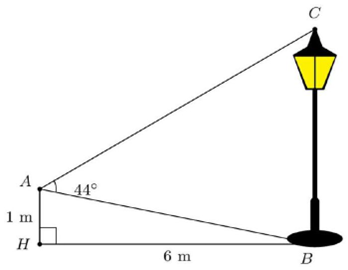
Bài 5: \({\rm{\;}}\) (2,0 điểm) Từ vị trí \({\rm{A}}\) cách mặt đất \(1{\rm{\;m}}\), một bạn nhỏ quan sát một cây đèn đường (hình vẽ). Biết \(HB = 6{\rm{\;m}},\widehat {BAC} = {44^ \circ }\). Tính chiều cao của cây đèn. (kết quả làm tròn đến hàng đơn vị)
Bài 6: (2,0 điểm) Hai chiếc tàu thủy cùng xuất phát từ vị trí \(A\), đi thẳng theo hai hướng tạo với nhau một góc \({50^ \circ }\). Tàu thứ nhất chạy với tốc độ \(30{\rm{\;km}}/{\rm{h}}\), tàu thứ hai chạy với tốc độ \(20{\rm{\;km}}/{\rm{h}}\). Hỏi sau \(2{\rm{\;h}}\), hai tàu cách nhau bao nhiêu km? (kết quả làm tròn đến hàng đơn vị)
Bài 7: \(\left( {1,0} \right.\) điểm) Cho tam giác \(ABC\) có \(BC = a,CA = b,AB = c\) thỏa mãn \(\dfrac{{a + b}}{2} = \dfrac{{b + c}}{3} = \dfrac{{c + a}}{5}\). Tính giá trị của biểu thức \(P = {\rm{cos}}A + 2{\rm{cos}}B + 4{\rm{cos}}C\).
ĐỀ 12: LÊ HỒNG PHONG
Bài 1: (3.0 điểm) Cho tam giác \(ABC\) có \(AB = 5,AC = 8\) và \(BC = 9\).
a) Tính côsin của góc \(B\) của tám giác \(ABC\).
b) Gọi \(M\) là trung điểm của \(BC\). Tính độ dài của đoạn \(AM\).
Bài 2: (2.0 điểm) Cho tam giác \(ABC\) nội tiếp đường tròn bán kính \(R,AB = R,AC = R\sqrt 3 \). Tính góc và tỉ số \(\dfrac{R}{{BC}}\) biết là góc tù.
Bài 3: (3.0 điểm) Cho tam giác \(ABC\) có \(a = 15,b = 13\) và \(c = 14\). Tính:
a) Diện tích tam giác \(ABC\).
b) Bán kính đường tròn ngoại tiếp tam giác \(ABC\).
Bài 4: (1.0 điểm) Cho tam giác \(ABC\) có cạnh \(AB = 14\), góc , tổng hai cạnh còn lại là 16 . Tính độ dài hai cạnh còn lại, biết \(BC > AC\).
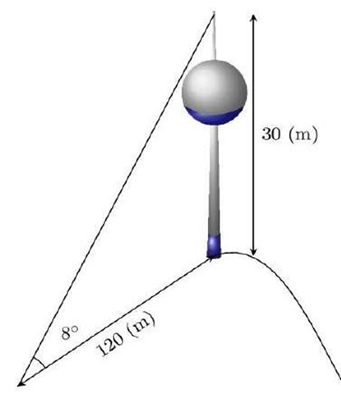
Bài 5: (1.0 điểm) Một tháp nước cao \(30\left( {{\rm{\;m}}} \right)\) ở trên đỉnh của một ngọn đồi. Từ tháp đến chân ngọn đồi dài \(120{\rm{\;m}}\) và người ta quan sát thấy góc tạo thành giữa đỉnh và chân tháp là \({8^ \circ }\). Hỏi góc nghiêng của ngọn đồi so với phương ngang là bao nhiêu? (Kết quả được làm tròn đến độ).
ĐỀ 13: LÊ THÁNH TÔNG
Bài 1: \((0,5\) điểm) Bất phương trình nào dưới đây là bất phương trình bậc nhất hai ẩn \(x,y\) ?
a) \(2x + y = 4 < 0\)
b) \( – 3x – {y^2} + 7 \ge 0\)
c) \(A – 4 > 0\).
d) \({x^2} + xy + 1 > 0\)
Bài 2: (1,0 điểm) Cặp số nào sau đây là nghiệm bất phương trình \(4x – 7y – 28 \ge 0\) ? Vì sao?
a) \(\left( {9,1} \right)\).
b) \(\left( {1; – 2} \right)\).
Bài 3: (1,0 điểm) Tìm tập xác định của hàm số \(y = f\left( x \right) = \dfrac{{{x^2} + 1}}{{2{x^2} – 5x + 2}}\).
Bài 4: \(\left( {1,0} \right.\) điểm) Xét tính đồng biến, nghịch biến của hàm số \(y = \dfrac{1}{{x – 1}}\) trên khoảng \(\left( {1; + \infty } \right)\).
Bài 5: (2,0 điểm) Trong hội chợ ẩm thực Xuân, lớp 10B1 được ban tổ chức cung cấp \(12\left( {{\rm{\;kg}}} \right)\) nguyên liệu loại \(A\) và \(8\left( {{\rm{\;kg}}} \right)\) nguyên liệu loại \(B\) để làm ra hai món ăn \(P\) và \(Q\). Để làm được \(1\left( {{\rm{\;kg}}} \right)\) món \(P\) cần dùng \(6\left( {{\rm{\;kg}}} \right)\) nguyên liệu \(A\) và \(2\left( {{\rm{\;kg}}} \right)\) nguyên liệu loại \(B\), khi bán lãi được 200 ngàn đồng. Để làm được \(1\left( {{\rm{\;kg}}} \right)\) món \(Q\) cần dùng \(2\left( {{\rm{\;kg}}} \right)\) nguyên liệu loại \(A\) và \(2\left( {{\rm{\;kg}}} \right)\) nguyên liệu loại \(B\), khi bán lãi được 100 ngàn đồng. Hāy cho biết lớp \(10{\rm{\;B}}1\) cần làm bao nhiêu \(\left( {{\rm{kg}}} \right)\) món ăn mỗi loại để khi bán thu được nhiều tiền nhất?
Bài 6: (2,5 điểm) Cho tam giác \(ABC\) có \(AB = 10,AC = 17,BC = 21\) và \(M\) là trung điểm \(BC\). Tính diện tích tam giác \(ABC\) và độ dài \(AM\), bán kính đường tròn nội tiếp tam giác \(ABC\) và bán kính đường tròn ngoại tiếp tam giác \(ABM\).
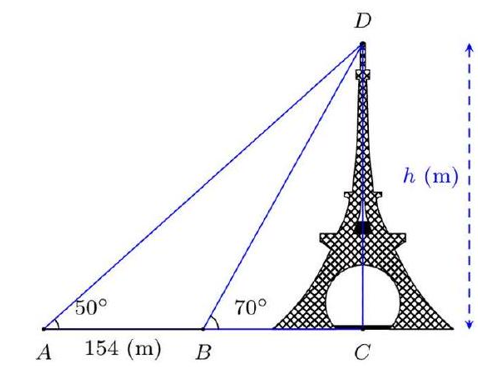
Bài 7: (1,0 điểm) Trong lần đến tham quan tháp Eiffel (ở Thư đô Paris, Pháp), bạn Nam muốn ước tính độ cao của tháp. Sau khi quan sát, bạn Nam đã minh hoạ lại kết quả đo đạc ở hình dưới \(AB = 154\left( {{\rm{\;m}}} \right),\widehat {DAB} = {50^ \circ },\widehat {DBC} = {70^ \circ }\). Em hãy giúp bạn Nam tính độ cao \(h\) của tháp Eiffel (làm tròn kết quả đến hàng đơn vị).
Bài 8: \((0,5\) điểm) Tìm tất cả các giá trị của tham số \(m\) để với mọi \(x\) thuộc đoạn \(\left[ {0;3} \right]\) hàm số \(y = f\left( x \right) = mx – 2m + 4\) nhận giá trị dương.
Bài 9: (0,5 điểm) Cho tam giác \(ABC\) có \(BC = a,AC = b,AB = c\) và thỏa \({\rm{tan}}\dfrac{A}{2} \cdot {\rm{tan}}\dfrac{B}{2} = \dfrac{1}{3}\). Chứng minh rằng: \(a + b = 2c\).


