Chào các bạn, vừa qua mình có dịp được tham gia tập huấn về cách ra đề thi 3 dạng thức (Trắc nghiệm nhiều lựa chọn, trắc nghiệm Đúng/Sai và câu trả lời ngắn) cùng với các chuyên gia của Bộ Giáo Dục và Đào tạo. nay mình viết bài này để chia sẻ lại với mọi người, đặc biệt là giáo viên để nhìn rõ hơn về cách đặt câu hỏi cũng như dạng thức mới cho kì thi tốt nghiệp THPT theo chương trình mới (CT 2018) sẽ bắt đầu từ 2025.
Ở đây Chân Đức sẽ tập trung nhiều về môn Toán, các môn tự nhiên khác cũng sẽ hoàn toàn tương tự thôi ạ, chỉ các về phân bổ số điểm.
Học sinh cũng có thể nắm được tinh thần cách ra đề thi đễ dễ hình dung công việc mình cần phải làm, rồi chúng ta bắt đầu vô việc luôn nha
1. Giới thiệu cấu trúc và 3 dạng thức câu hỏi
Đầu tiên cấu trúc đề thi môn Toán như sau:
| Loại câu hỏi — Số lệnh hỏi và điểm | Số câu | Số lệnh hỏi/câu | Số điểm/lệnh hỏi | Số điểm/câu | Tổng số điểm |
|---|---|---|---|---|---|
| Câu trắc nghiệm nhiều phương án lựa chọn (trong 4 phương án có 1 phương án đúng) | 12 | 1 | 0,25 | 0,25 | 3,0 |
| Câu trắc nghiệm đúng sai | 4 | 4 | Theo qui tắc (*) | 1 | 4,0 |
| Câu trắc nghiệm yêu cầu trả lời ngắn | 6 | 1 | 0,5 | 0,5 | 3,0 |
Ghi chú: Qui tắc (*) như sau: mỗi câu trắc nghiệm đúng-sai có 4 ý a), b), c), d), với mỗi ý chỉ chọn Đúng hoặc Sai. Thí sinh lựa chọn chính xác 1 ý trong số 4 ý thì được 0,1 điểm, 2 ý được 0,25, 3 ý được 0,5 và 4 ý được 1 điểm.
1.1. Dạng thức 1: Trắc nghiệm nhiều lựa chọn
Đây là dạng câu hỏi quen thuộc như chương trình thi trước đây, với mỗi câu hỏi học sinh chọn một phương án duy nhất.
Ví dụ 1. Phát biểu nào sau đây là đúng?
A. \(\int(3^x)dx = 3^x\).
B. \(\int(3^x)dx = 3^x \ln{3} + C\).
C. \(\int(3^x)dx = \dfrac{3^x}{\ln{3}} + C\).
D. \(\int{3^x}dx = 3^x + C\)
Lời bình. Đây là những câu hỏi khá quen thuộc với hình thức trắc nghiệm bấy lâu nay, thuộc nội dung nguyên hàm lớp 12, đáp án trong trường hợp này là C.
Ví dụ 2. Công ty nước giải khát (X) tổ chức một chương trình khuyến mại như sau: Trong mỗi thùng 24 chai nước giải khát đều có hai chai trúng thưởng (giải thưởng được viết ở dưới nắp chai), người tham gia chương trình được mở nắp một cách ngẫu nhiên lần lượt hai chai trong một thùng. Tính xác suất để một người tham gia chương trình mở được cả hai chai đều trúng thưởng. (Trích SGK Cùng Khám Phá Toán 12)
A. \(\dfrac{1}{12}\)
B. \(\dfrac{1}{576}\)
C. \(\dfrac{1}{552}\)
D. \(\dfrac{1}{276}\)
Lời bình. Đây là một câu liên quan đến mạch xác suất, tuy nhiên bài này là xác suất có điều kiện, học sinh sẽ được học ở lớp 12 từ năm học 2025. Đáp án là: \(\dfrac{1}{276}\)
1.2. Dạng thức 2: Trắc nghiệm Đúng/Sai
Ở dạng thức câu hỏi này mỗi câu hỏi sẽ có 4 ý a), b), c) d). Ở mỗi ý a), b), c), d) học sinh chọn Đúng hoặc Sai, nghĩa là trong một câu hỏi có 4 lệnh hỏi, có thể hiểu và ra đề một trong hai hướng sau đây:
Hướng 1: Có một giả thiết ban đầu và 4 ý a), b), c), d) độc lập nhau cùng sử dụng liên quan đến giả thiết ban đầu đó. Xem ví dụ 3.
Hướng 2: Có một giả thiết ban đầu và 4 ý a), b), c), d) sẽ có ý đồ nối tiếp nhau giúp học sinh có thể khám phá ra một định lí, kết quả, tính chất Toán học nào đó. Xem ví dụ 4.
Ví dụ 3. Câu hỏi Đúng-sai theo Hướng 1, các ý độc lập
Cho các hàm số \(f(x)\) và \(g(x)\) thoả mãn \(f^{\prime}(x)=2 x+1\) và \(g^{\prime}(x)=x, \forall x \in \mathbb{R}\).
a) \([f(x)+g(x)]^{\prime}=3 x+1\).
b) \([f(x)-g(x)]^{\prime}=x+1\).
c) \([5 f(x)]^{\prime}=2 x+6\)
d) \([-7 g(x)]^{\prime}=-7+x\).
Lời bình. Ở đây, với giả thiết đã cho về \(f ^\prime (x)\), \(g^ \prime (x)\), các ý a), b), c) d) là việc sử dụng quy tắc đạo hàm (cộng, trừ, nhân) độc lập nhau, ý nào thực hiện trước đều được, đáp án cho ví dụ này là: a) Đúng, b) Đúng, c) Sai, d) Sai.
Ví dụ 4. Câu hỏi đúng sai theo Hướng 2 mạch liên kết có dụng ý
Cho hàm số \(y=f(x)=x^3-3 x\).
a) Tập xác định của hàm số đã cho là \(\mathbb{R}\).
b) \(f^{\prime}(x)=3 x^2+3\)
c) \(f^{\prime}(x)<0\) khi \(x \in(-\infty ;-1) \cup(1 ;+\infty)\), \(f^{\prime}(x)>0\) khi \(x \in(-1 ; 1)\).
d) Hàm số đã cho có đồ thị như ở hình bên.
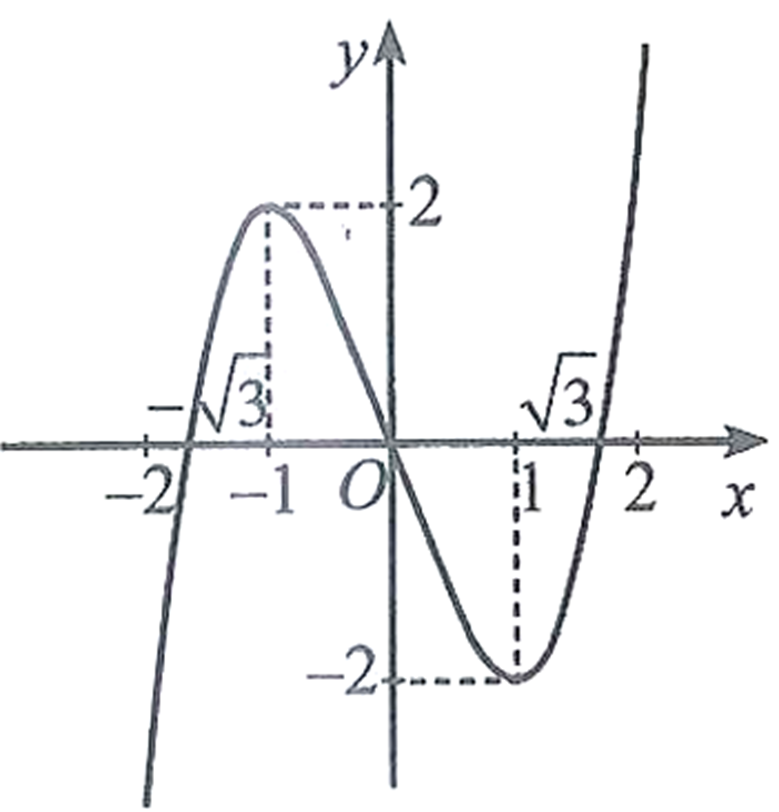
Lời bình. Ở đây, dụng ý của tác giả là muốn học sinh theo một mạch kiến thức trong việc khảo sát và vẽ đồ thị hàm số bậc 3: \(y=ax^3+bx^2+cx+d\), và theo trình tự suy nghĩ cho các ý a), b), c), d) này là học sinh đang từng bước chiếm lĩnh tri thức về các bước khảo sát và vẽ đồ thị hàm số này. Ý cuối cùng d) chính là mục tiêu đạt được sau các bước a), b), c) ở trên.
Đáp án câu này là: a) Đúng b) Sai c) Sai d) Đúng.
Ghi chú: Sẽ có thắc mắc rằng, liệu câu hỏi Đúng-Sai có thể trộn các ý a), b), c), d) được không? thì câu trả lời là tùy theo hướng tiếp cận của câu hỏi đó. Nếu tiếp cận theo Hướng 1 thì trộn thoải mái, nhưng nếu đề tiếp cận theo Hướng 2 thì tuyệt đối không được trộn.
1.3. Dạng thức 3: Trắc nghiệm trả lời ngắn
Ở dạng thức này, thực chất là một câu tự luận trước đây, nhưng học sinh không cần phải trình bày lời giải mà chỉ điền kết quả. Và do đó, kết quả của mỗi câu hỏi này tất nhiên chỉ là số. Điều này phù hợp với việc học sinh tô vào phiếu trả lời trắc nghiệm

Có nhiều thủ thuật để đáp số là số nguyên (âm hoặc dương) hoặc số thập phân, làm sao tối đa 4 số, chẳng hạn, nếu kết quả chúng ta trong một bài thể tích là \(V=\dfrac{\sqrt{2}}{3}\) thì ta có thể hỏi giá trị của \(9V^2\) là: …. lúc đó, học sinh hoàn toàn có thể điền là 2.
Hoặc trong một số bài toán thực tế, cách đơn giản nhất là dùng số qui tròn. Xem ví dụ 6
Ví dụ 5. Cho hình chóp \(S . A B C D\) có đáy là hình vuông cạnh \(a\), \(S A \perp(A B C D)\), số đo của góc nhị diện \([S, B C, A]\) bằng \(60^{\circ}\). Khoảng cách giữa hai đường thẳng \(S C\) và \(B D\) bằng \(\dfrac{a \sqrt{30}}{n}\) (\(n\) là số tự nhiên). Giá trị của \(n\) bằng bao nhiêu?
Lời bình. Đây là bài liên quan khoảng cách trong hình học không gian (quan hệ vuông góc) ở lớp 11, và thường các kết quả này sẽ phải là số nguyên, nhưng ta vẫn có cách để học sinh trả lời bằng một số nguyên hoặc số tự nhiên. Đáp số bài này, giá trị của \(n\) bằng 10.
Ví dụ 6. Trong một thí nghiệm, một quả cầu được gắn vào một đầu dây đàn hồi, đầu kia của sợi dây được gắn cố định vào một thanh treo nằm ngang. Sau khi quả cầu được kéo xuống và thả ra, nó bắt đầu di chuyển lên xuống. Khi đó, chiều cao \(h(\mathrm{~cm})\) của quả cầu so với mặt đất theo thời gian (t(s)) được cho bởi công thức $$h=100-30 \cos 20 t .$$ Tính thời điểm đầu tiên mà quả cầu đạt chiều cao cao nhất kể từ khi quả cầu được thả ra (làm tròn kết quả đến hàng phần trăm).
Lời bình. Bài toán này liên quan đến kiến thức về lượng giác ở lớp 11, hs có thể giải là: Do \(-1 \leq \cos 20 t \leq 1\) nên \(70 \leq 100-30 \cos 20 t \leq 130\). Ta có \(h=130 \mathrm{~cm}\) khi
\(\cos 20 t=-1 \Leftrightarrow 20 t=\pi+k 2 \pi \Leftrightarrow t=\frac{\pi}{20}+k \frac{\pi}{10} \text { với } k \in \mathbb{N} \)
Vậy thời điểm đầu tiên mà quả cầu đạt chiều cao cao nhất kể từ khi quả cầu được thả ra là \(t=\dfrac{\pi}{20} \approx 0,16\) (s).
Từ đó tô vào phiếu giá trị 0,16
Ví dụ 7. Một quả bóng được thả thẳng đứng từ độ cao \(10 \mathrm{~m}\) rơi xuống đất và nảy lên. Giả sử sau mỗi một lần rơi xuống, nó nảy lên được một độ cao bằng \(75 \%\) độ cao vừa rơi xuống. Tính tổng quãng đường quả bóng di chuyển được kể từ lúc thả xuống đến khi quả bóng chạm đất lần thứ 10 (làm tròn kết quả đến hàng phần mười của mét).
Trong ví dụ 6 học sinh có thể giải là \(S=10+2\left(u_1+u_2+\ldots+u_9\right) \)
\(=10+2 \cdot 7,5 \cdot \dfrac{1-(0,75)^9}{1-0,75} \approx 65,5(\mathrm{~m})\).
Đáp số cần tô vào phiếu là 65,5
Tuy nhiên, đây là suy nghĩ riêng của mình nha: những câu hỏi như Ví dụ 7 này cần cân nhắc, bởi lẽ việc tính toán làm tròn có những khâu trung gian, có thể sẽ gây tranh cãi khi có học sinh điền không đúng ý đồ, chẳng hạn là 64,0 (bạn đọc hãy xem tại sao nhé)
2. Quy trình xây dựng ma trận và câu hỏi
Đây cũng chủ đề hay, để có thời gian mình sẽ ghi kĩ hơn, tạm thời mình tóm tắt như thế này, có 2 tiến trình để xây dựng ma trận và câu hỏi như sau (thông thường Tiến trình 2 quen thuộc với chúng ta hơn, và dễ làm hơn)
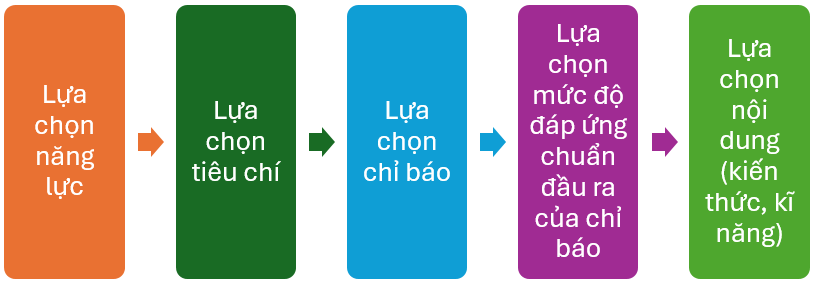
Tiến trình 1:
Với mỗi chỉ báo cốt lõi đã được lựa chọn và mức độ đáp ứng chuẩn đầu ra của chỉ báo đó đã được xác định, ta tìm nội dung môn học (kiến thức, kĩ năng) phản ánh tốt nhất chỉ báo và mức độ đáp ứng chuẩn đầu ra của chỉ báo đó để đưa vào ma trận của đề đánh giá.
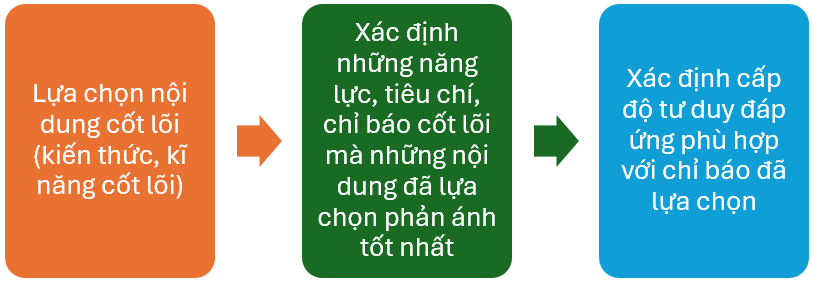
Tiến trình 2:
Bước 1. Xác định nội dung kiến thức (từ một hoặc nhiều đơn vị kiến thức) để xây dựng bối cảnh “có ý nghĩa”
Bước 2. Xác định những năng lực, tiêu chí, chỉ báo cốt lõi mà những nội dung đã lựa chọn phản ánh tốt nhất.
Bước 3. Xác định cấp độ tư duy đáp ứng phù hợp với chỉ báo đã lựa chọn cũng như phù hợp với nội dung kiến thức thể hiện ở bối cảnh đặt ra/xây dựng.
Bước 4. Điều chỉnh bối cảnh (khi cần thiết) và lệnh hỏi để phù hợp với các biểu hiện của năng lực và cấp độ tư duy cần đánh giá.
3. Hiểu rõ về “mô hình hóa Toán học”
Phần này để có thời gian mình sẽ viết thêm nha, đây cũng là điều rất hay, lí giải vì sao hiện tại một số bài toán thực tế đôi khi nó chỉ mang mô hình thực tế, v.v….
4. Bàn luận thêm một chút về cách đánh giá năng lực
Có nhiều định nghĩa về năng lực, và tất nhiên mình không phải chuyên gia để đưa ra hết ở đây, nhưng mình hiểu đơn giản theo “Mô hình tảng băng về cấu trúc năng lực“, và người ta có thể hiểu như sau

Cấu trúc năng lực ở hình trên gồm 3 tầng: tầng 1 là tầng LÀM, tầng những gì mà cá nhân thực hiện được, làm được vì thế nên có thể quan sát được. Tầng 2 là SUY NGHĨ, tầng tiền đề, tức là những kiến thức, kỹ năng tư duy cùng với giá trị niềm tin là cơ sở quan trọng để phát triển tư duy, suy nghĩ… là điều kiện để phát triển năng lực, chúng ở dạng tiềm năng, không quan sát được. Tầng 3 là tầng MONG MUỐN, tầng sâu nhất, quyết định cho sự khởi phát và tính độc đáo của năng lực được hình thành, trong đó động cơ và tính tích cực của nhân cách có tính quyết định. Bởi nếu bạn thực sự mong muốn, bạn có thể đạt được những điều ở tầng 2 và 1; nếu bạn không muốn thì không gì có thể thay đổi bạn. Tầng 1 vừa là tầng thể hiện kết quả của hoạt động (thể hiện năng lực) và vừa là con đường và phương thức hình thành và phát triển năng lực.
To be continue




