Bài viết này hướng đến phân tích một số câu hỏi không rõ nghĩa, có thể dẫn đến các kết quả khác nhau.
Ví dụ 1. Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { – 20;20} \right]\) để bất phương trình \({\log _3}{x^2} + m\sqrt {{{\log }_3}{x^3}} + m + 1 \le 0\) có không quá 20 nghiệm nguyên?
A. 23. ***** B. 20. ***** C. 21. ***** D.22.
Bình luận
Chưa nói đến bài giải, ở đây ta thắc mắc rằng câu “có không quá 20 nghiệm nguyên” là có bao gồm luôn trường hợp vô nghiệm? Thực ra hiểu theo nghĩa nào cũng có lý.
Hiểu theo ý bao gồm cả vô nghiệm hợp lý vì xem như có 0 nghiệm mà 0 nghiệm tức là có ít hơn 20 nghiệm rồi.
Hiểu theo ý không tính vô nghiệm cũng hợp lý, vì rằng đã có từ “có” ở đây, nếu mà vô nghiệm chẳng khác nào câu này thành “có không có nghiệm” !!!! thật là kì.
Bây giờ, với hai cách hiểu đó ta sẽ đi đến lời giải sau đây.
Hướng dẫn.
Điều kiện của bài toán là \(x>0\) và \(\log_3{x} \geq 0\) hay nói cách khác \(x \geq 1\).
Để cho tiện, trong bài này ta sẽ cô lập \(m\), bất phương trình đã cho tương đương với
\[m \leq \dfrac{-2log_3{x}-1}{\sqrt{3log_3{x}}+1}\]
(ở trên do \(x \geq 1\) nên ta chia thoải mái con nhái \(\sqrt{3log_3{x}}+1\) mà không phải lo đổi chiều bpt gì cả).
Đặt \(g(x) = \dfrac{-2log_3{x}-1}{\sqrt{3log_3{x}}+1}\) ta có
\(g(t) = \dfrac{\frac{-2}{3}t^2-1}{t+1}=\dfrac{-2t^2-3}{3(t+1)}\) ở đây ta đã đặt \(t=\sqrt{3log_3{x}}\) cho tiện và chú ý rằng \(t^\prime = \dfrac{3.\dfrac{1}{xln3}}{2\sqrt{3log_3{x}}}\) luôn là số dương rồi. Do vậy ta có:
\(g ^\prime = \dfrac{1}{3}.\dfrac{-2t^2-4t+3}{(t+1)^2}.t ^ \prime\)
\(g ^ \prime (t)=0\) khi \(t=\dfrac{-2\pm \sqrt{10}}{2}\) nên ta có bảng biến thiên như sau:
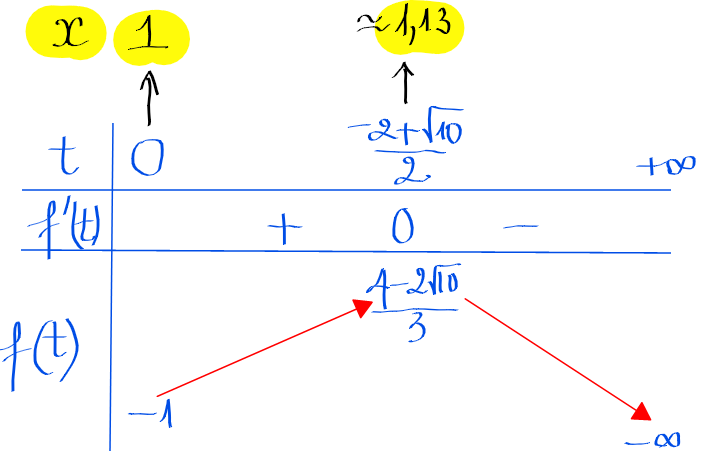
Chú ý rằng: khi \(t=0\) ta có \(\sqrt{3log_3{x}}=0 \Leftrightarrow x =1\), tương tự khi \(t=\frac{-2+\sqrt{10}}{2}\) ta có \(\sqrt{3log_3{x}}=\frac{-2+\sqrt{10}}{2}\) tức mình giải được \(x\) xấp xỉ \(1,13\).
theo bảng biến thiên này ta thấy khi \(t\) chạy từ 0 đến \(+\infty\) thì ta có \(x\) chạy từ 1 ra \(+\infty\), theo đề bài ta chỉ có không quá 20 nghiệm nguyên nên ta chặn ngay chỗ \(x=21\) theo bảng minh họa sau (chú ý phần màu vàng là của \(x\):
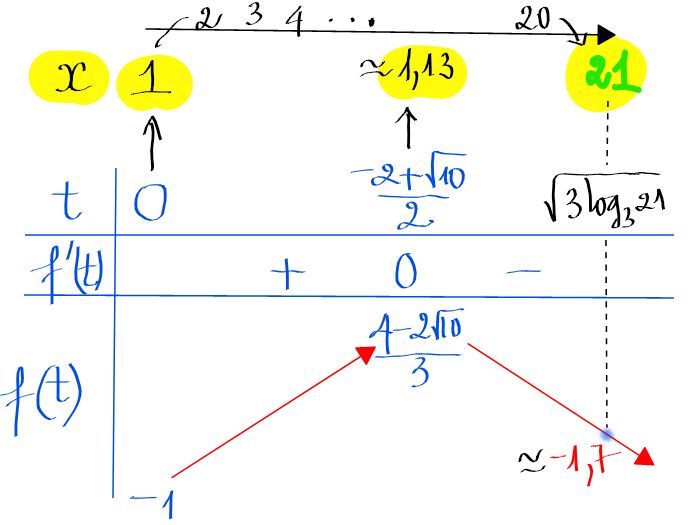
Như vậy, chắc chắn một điều là đường \(y=m\) không được thấp hơn số \(-1,7\) vì nếu thấp hơn sẽ có nhiều hơn 20 nghiệm nguyên mất.
Lúc này, tùy theo cách hiểu mà ta có đáp số như sau:
+ Nếu hiểu theo nghĩa bao gồm cả trường hợp vô nghiệm thì \(m\) chỉ cần cao hơn \(-1,7\), thậm chí có thể cao hơn số \(\frac{4-2\sqrt{10}}{3}\) nên ta có các \(m\) thỏa bài toán là những giá trị nguyên sao cho lớn hơn \(-1,7\) ta có \(m\in \{-1; 0; 1; 2; …; 20\}\) có 22 giá trị \(m\) cần tìm.
+ Nếu hiểu theo nghĩa không bao gồm trường hợp vô nghiệm thì \(m\) cần cao hơn \(-1,7\) nhưng phải \( \leq \frac{4-2\sqrt{10}}{3}\) tức \(m \leq -0,77\) mà \(m\) là số nguyên nên ta có \(-1 \leq m \leq -1\) hay \(m=-1\), đáp số là có 1 giá trị \(m\) cần tìm.
Dựa theo các đáp án thì ta hiểu ý tác giả rồi đấy, và phải chọn phương án D.22.
Ví dụ 2. Một hộp đựng 5 viên bi đỏ và 4 viên bi vàng. Có bao nhiêu cách chọn ra 3 viên bi sao cho số bi đỏ nhiều hơn số bi vàng.
Thảo luận.
Ta dễ thấy rằng, để lấy 3 viên bi sao cho số bi đỏ lớn hơn số bi vàng thì có thể có các trường hợp sau:
Th1. 3 bi đỏ và 0 bi vàng.
Tất nhiên có \(C_5^3.C_4^0=10\) cách.
Th2. 2 bi đỏ và 1 bi vàng
Tất nhiên có \(C_5^2. C_4^1=40\) cách.
Tuy nhiên ở trường hợp 1 nó rất là kì ở chỗ “0 bi vàng”, mặc dù \(3>0\) thì đúng rồi, nhưng theo giả thiết là lấy bi (chọn bi) mà, chẳng lẽ đi “lấy ra 0 bi” nghĩa là sao? đã lấy mà lại không có tức không lấy???
Cho nên, đáng lẽ đề bài cần hỏi rõ ràng hơn, đại khái như:
“Có bao nhiêu cách chọn ra 3 viên bi đủ cả hai màu, sao cho số bi đỏ nhiều hơn số bi vàng” tức là không có Th1 thì hợp lí hơn.



