Cho hình tứ diện đều \(ABCD\) có cạnh bằng \(a\). Lấy điểm \(M\) bất kì nằm ở miền trong của tứ diện. Tính:
\(T=d(M, (BCD)) + d(M, (ACD)) + d(M,(ABD))+ d(M, (ABC)) \)
Giải
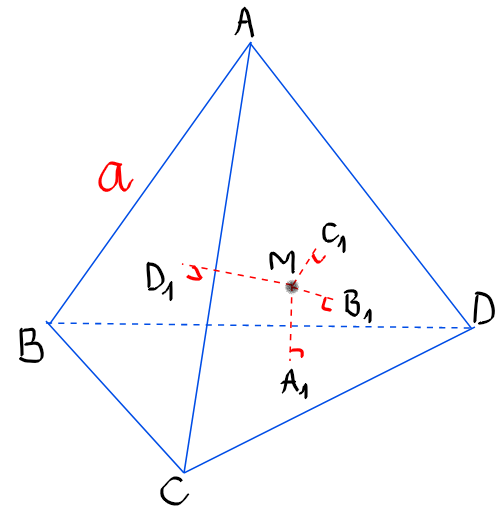
Gọi \(A_1, B_1, C_1, D_1\) lần lượt là hình chiếu của điểm \(M\) lên các mặt phẳng \((BCD), (ACD), (ABD), (ABC)\)
Ta có: \(T=d(M, (BCD)) + d(M, (ACD)) + d(M,(ABD))+ d(M, (ABC))\)
\(=MA_1+MB_1+MC_1+MD_1 \)
Ta có: \(V_{MBCD}=\dfrac{1}{3}.MA_1.S_{BCD} \)
\(\Rightarrow d(M, (BCD)) = MA_1 = \dfrac{3V_{MBCD}}{S_{BCD}}\)
Tương tự như vậy cho \(MB_1, MC_1,MD_1\), ta có:
\(T=MA_1+MB_1+MC_1+MD_1\)
\(=\dfrac{3V_{MBCD}}{S_{BCD}}+\dfrac{3V_{MACD}}{S_{ACD}}+\dfrac{3V_{MABD}}{S_{ABD}}+\dfrac{3V_{MABC}}{S_{ABC}}\)
mà \(S_{BCD}=S_{ACD}=S_{ABD}=S_{ABC}=S=\dfrac{a^2\sqrt3}{4}\)
nên \(T=\dfrac{3}{S} \left(V_{MBCD}+V_{MACD}+V_{MABD}+V_{MABC}\right)\)
\(=\dfrac{3}{S}.V_{ABCD}\)
Ta dễ dàng tính được \(V_{ABCD}=\dfrac{a^3\sqrt{2}}{12}\)
nên ta có:
\(T=\dfrac{3}{\frac{a^2\sqrt3}{4}}.\dfrac{a^3\sqrt{2}}{12}\)
\(=\dfrac{a\sqrt{6}}{3}\)
Lời bình
Bài này ý tưởng xuất phát từ việc chiều cao có thể tính thông qua thể tích. Cụ thể là:
\(V=\dfrac{1}{3}.S_{đ}.h \Leftrightarrow h = \dfrac{3V}{S_{đ}}\)



